Bài tập 7 trang 70 SGK Hình học 10 NC
Bài tập 7 trang 70 SGK Hình học 10 NC
Cho tam giác ABC. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là b2+c2 = 5a2
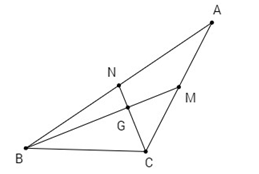
Gọi G là giao điểm của hai trung tuyến BM, CN.
Áp dụng công thức tính trung tuyến ta có:
\(\begin{array}{*{20}{l}}
{G{B^2} = \frac{4}{9}B{M^2} = \frac{1}{9}\left( {2{a^2} + 2{c^2} - {b^2}} \right)}\\
{G{C^2} = \frac{4}{9}C{N^2} = \frac{1}{9}\left( {2{a^2} + 2{b^2} - {c^2}} \right)}
\end{array}\)
Do đó \(\begin{array}{*{20}{l}}
{G{B^2} = \frac{4}{9}B{M^2} = \frac{1}{9}\left( {2{a^2} + 2{c^2} - {b^2}} \right)}\\
{G{C^2} = \frac{4}{9}C{N^2} = \frac{1}{9}\left( {2{a^2} + 2{b^2} - {c^2}} \right)}
\end{array}\)
\(\begin{array}{*{20}{l}}
{ \Leftrightarrow \frac{1}{9}\left( {2{a^2} + 2{c^2} - {b^2}} \right) + \frac{1}{9}\left( {2{a^2} + 2{b^2} - {c^2}} \right) = {a^2}}\\
{ \Leftrightarrow 4{a^2} + {b^2} + {c^2} = 9{a^2}}\\
{ \Leftrightarrow {b^2} + {c^2} = 5{a^2}}
\end{array}\)
-- Mod Toán 10
Copyright © 2021 HOCTAP247
