Bài tập 12 trang 71 SGK Hình học 10 NC

Bài tập 12 trang 71 SGK Hình học 10 NC

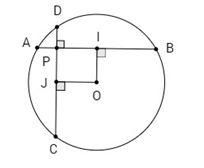
a) Gọi I, J lần lượt là trung điểm của AB, CD.

Ta có OI⊥AB; OJ⊥CD

Suy ra OIPJ là hình chữ nhật. Ta có:

\(\begin{array}{l}
A{B^2} + C{D^2} = 4\left( {A{I^2} + C{J^2}} \right)\\
 = 4\left( {O{A^2} - O{I^2} + C{O^2} - J{O^2}} \right)
\end{array}\)

\( = 4\left( {2{R^2} - O{P^2}} \right)\) (không đổi do cố định)

b) Ta có:

\(\begin{array}{*{20}{l}}
{P{A^2} + P{B^2} + P{C^2} + P{D^2}}\\
\begin{array}{l}
 = {\left( {\overrightarrow {PA}  - \overrightarrow {PB} } \right)^2} + {\left( {\overrightarrow {PC}  - \overrightarrow {PD} } \right)^2}\\
 + 2.\overrightarrow {PA} .\overrightarrow {PB}  + 2\overrightarrow {PC} .\overrightarrow {PD} 
\end{array}\\
{ = A{B^2} + C{D^2} + 4\left( {P{O^2} - {R^2}} \right)}\\
{ = 4\left( {2{R^2} - O{P^2}} \right) + 4\left( {P{O^2} - {R^2}} \right) = 4{R^2}}
\end{array}\)

Vậy \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P.

-- Mod Toán 10