Bài tập 30 trang 66 SGK Hình học 10 NC

Bài tập 30 trang 66 SGK Hình học 10 NC

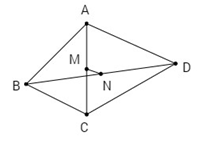
Áp dụng công thức tính trung tuyến, MN là trung tuyến của tam giác BMD, ta có:

\(\begin{array}{l}
M{N^2} = \frac{{B{M^2} + D{M^2}}}{2} - \frac{{B{D^2}}}{4}\\
 \Leftrightarrow 4M{N^2} = 2\left( {B{M^2} + D{M^2}} \right) - B{D^2}\left( 1 \right)
\end{array}\)

Tương tự, BM, DM lần lượt là trung tuyến của tam giác ABC, ADC nên:

\(\begin{array}{l}
4B{M^2} = 2\left( {A{B^2} + B{C^2}} \right) - A{C^2}\,\,\,\left( 2 \right)\\
4D{M^2} = 2\left( {D{A^2} + C{D^2}} \right) - A{C^2}\,\,\left( 3 \right)
\end{array}\)

Từ (2), (3) suy ra:

\(\begin{array}{l}
2\left( {B{M^2} + D{M^2}} \right)\\
 = A{B^2} + B{C^2} + C{D^2} + D{A^2} - A{C^2}{\mkern 1mu} {\mkern 1mu} \left( 4 \right)
\end{array}\)

Thay (4) vào (1), ta có

4MN² = AB²+BC²+CD²+DA²−AC²−BD² 

⇒ AB²+BC²+CD²+DA² = AC²+BD²+4MN²

-- Mod Toán 10