Bài tập 10 trang 52 SGK Hình học 10 NC
Bài tập 10 trang 52 SGK Hình học 10 NC
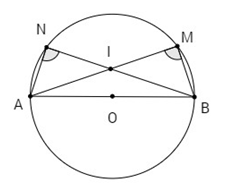
Cho hai điểm M, N nằm trên đường tròn đường kính AB = 2R. Gọi I là giao điểm của hai đường thẳng AM, BN.
a) Chứng minh rằng \(\overrightarrow {AM} .\overrightarrow {AI} = \overrightarrow {AB} .\overrightarrow {AI} ;\overrightarrow {BN} .\overrightarrow {BI} = \overrightarrow {BA} .\overrightarrow {BI} \)
b) Tính \(\overrightarrow {AM} .\overrightarrow {AI} + \overrightarrow {BN} .\overrightarrow {BI} \) theo R.
a) Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AM} .\overrightarrow {AI} = \left( {\overrightarrow {AB} + \overrightarrow {BM} } \right).\overrightarrow {AI} \\
= \overrightarrow {AB} .\overrightarrow {AI} + \overrightarrow {BM} .\overrightarrow {AI} \\
= \overrightarrow {AB} .\overrightarrow {AI} \left( {do\overrightarrow {BM} .\overrightarrow {AI} = 0} \right)
\end{array}\\
\begin{array}{l}
\overrightarrow {BN} .\overrightarrow {BI} = \left( {\overrightarrow {BA} + \overrightarrow {AN} } \right).\overrightarrow {BI} \\
= \overrightarrow {BA} .\overrightarrow {BI} + \overrightarrow {AN} .\overrightarrow {BI} \\
= \overrightarrow {BA} .\overrightarrow {BI} \left( {do\overrightarrow {AN} .\overrightarrow {BI} = 0} \right)
\end{array}
\end{array}\)
b) Theo câu a), ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AM} .\overrightarrow {AI} + \overrightarrow {BN} .\overrightarrow {BI} \\
= \overrightarrow {AB} .\overrightarrow {AI} + \overrightarrow {BA} .\overrightarrow {BI}
\end{array}\\
\begin{array}{l}
= \overrightarrow {AB} \left( {\overrightarrow {AI} - \overrightarrow {BI} } \right)\\
= \overrightarrow {AB} .\overrightarrow {AB} = A{B^2} = 4{R^2}
\end{array}
\end{array}\)
-- Mod Toán 10
Copyright © 2021 HOCTAP247
