Bài tập 2 trang 91 SGK Toán 11 NC

Bài tập 2 trang 91 SGK Toán 11 NC

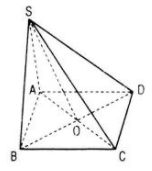
a) Ta có:

\(\begin{array}{*{20}{l}}
{\overrightarrow {SB}  + \overrightarrow {SD}  = \overrightarrow {SA}  + \overrightarrow {SC} }\\
\begin{array}{l}
 \Leftrightarrow \overrightarrow {SB}  - \overrightarrow {SC}  = \overrightarrow {SA}  - \overrightarrow {SD} \\
 \Leftrightarrow \overrightarrow {CB}  = \overrightarrow {DA} 
\end{array}
\end{array}\)

⇔ ABCD là hình bình hành

b) Ta có:

\(\begin{array}{*{20}{l}}
{\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {SD}  = 4\overrightarrow {SO} }\\
\begin{array}{l}
 \Leftrightarrow \overrightarrow {SO}  + \overrightarrow {OA}  + \overrightarrow {SO}  + \overrightarrow {OB}  + \overrightarrow {SO} \\
 + \overrightarrow {OC}  + \overrightarrow {SO}  + \overrightarrow {OD}  = 4\overrightarrow {SO} 
\end{array}\\
{ \Leftrightarrow \overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \vec 0{\mkern 1mu} (*)}
\end{array}\)

Nếu ABCD là hình bình hành thì 

\(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow 0 \)

Suy ra \(\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {SD}  = 4\overrightarrow {SO} \)

Ngược lại, giả sử 

\(\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {SD}  = 4\overrightarrow {SO} \) ta có (*)

Gọi M, N lần lượt là trung điểm của AC, BD thì 

\(\overrightarrow {OA}  + \overrightarrow {OC}  = 2\overrightarrow {OM} ,\)

\(\overrightarrow {OB}  + \overrightarrow {OD}  = 2\overrightarrow {ON} \)

Từ (*) suy ra \(2\left( {\overrightarrow {OM}  + \overrightarrow {ON} } \right) = \overrightarrow 0 \), suy ra O, M, N thẳng hàng.

Mặt khác, M thuộc AC, N thuộc BD và O là giao điểm của AC và BD nên O, M, N thẳng hàng chỉ xảy ra khi O ≡ M ≡ N, tức O là trung điểm AC và BD, hay ABCD là hình bình hành.

-- Mod Toán 11