Bài tập 33 trang 118 SGK Hình học 11 NC

Bài tập 33 trang 118 SGK Hình học 11 NC

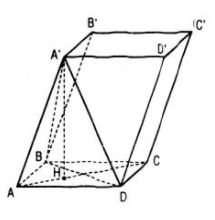
Từ giả thiết suy ra các tam giác A’AD, BAD, A’AB là các tam giác cân cùng có góc ở đỉnh bằng 600 nên chúng là các tam giác đều. Như vậy tứ diện A’ABD có các cạnh cùng bằng a hay A’ABD là tứ diện đều. Khi đó hình chiếu của A’ trên mp(ABCD) chính là trọng tâm H của tam giác đều ABD. Khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’) chính là độ dài A’H. Ta có:

\(\begin{array}{l}
A\prime {H^2} = AA{\prime ^2} - A{H^2}\\
 = {a^2} - {\left( {\frac{{a\sqrt 3 }}{3}} \right)^2} = {a^2} - \frac{{{a^2}}}{3} = \frac{{2{a^2}}}{3}
\end{array}\)

Vậy \(A\prime H = \frac{{a\sqrt 6 }}{3}\)

-- Mod Toán 11