Bài tập 11 trang 96 SGK Hình học 11 NC
Bài tập 11 trang 96 SGK Hình học 11 NC
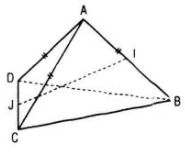
Cho hình tứ diện ABCD có AB = AC = AD và \(\widehat {BAC} = {60^0},\widehat {BAD} = {60^0}.\)
Chứng minh rằng :
a. AB ⊥ CD;
b. Nếu I và J lần lượt là trung điểm của AB và CD thì IJ ⊥ AB và IJ ⊥ CD.
a) Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right)\\
= \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC}
\end{array}\\
\begin{array}{l}
= AB.AD.\cos \widehat {BAD} - AB.AC\\
.\cos \widehat {BAC} = 0
\end{array}\\
{ \Rightarrow AB \bot CD.}
\end{array}\)
b)
Ta có:
\(\begin{array}{*{20}{l}}
{\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AJ} }\\
{ = \frac{1}{2}\overrightarrow {BA} + \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {AC} } \right)}\\
{ = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)}\\
{ = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {AC} - \overrightarrow {AB} } \right)}\\
\begin{array}{l}
\Rightarrow \overrightarrow {AB} .\overrightarrow {IJ} \\
= \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} - \overrightarrow {AC} - A{B^2}} \right)
\end{array}\\
\begin{array}{l}
= \frac{1}{2}(AB.AD.\cos {60^0} + AB.AC\\
.\cos {60^0} - A{B^2}) = 0
\end{array}\\
{ \Rightarrow AB \bot IJ}
\end{array}\)
Mặt khác:
\(\begin{array}{*{20}{l}}
{\overrightarrow {CD} .\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right).\left( {\overrightarrow {AD} + \overrightarrow {BA} + \overrightarrow {AC} } \right)}\\
\begin{array}{l}
= \frac{1}{2}( - \overrightarrow {AC} .\overrightarrow {AD} + {\overrightarrow {AD} ^2} + \overrightarrow {CA} .\overrightarrow {BA} \\
+ \overrightarrow {AD} .\overrightarrow {BA} - {\overrightarrow {AC} ^2} + \overrightarrow {AD} .\overrightarrow {AC} )
\end{array}\\
{ = - \frac{1}{2}\overrightarrow {AB} .\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right) = - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {CD} = 0}\\
{ \Rightarrow CD \bot IJ}
\end{array}\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
