Bài tập 11 trang 114 SGK Hình học 11

Bài tập 11 trang 114 SGK Hình học 11

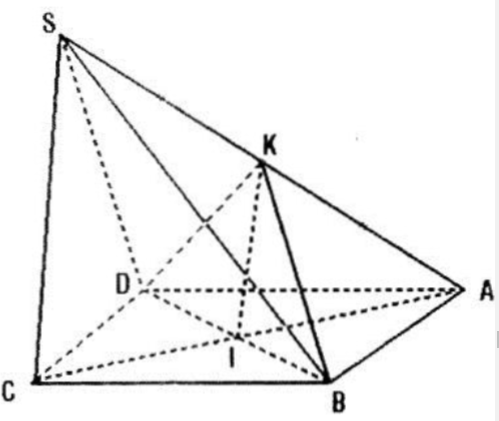
Câu a:

Vì ABCD là hình thoi \(\Rightarrow AC \perp BD \ (1)\)

Theo giả thiết \(SC\perp (ABCD)\)

\(\Rightarrow SC\perp BD (2)\)

Từ (1) và (2) \(BD\perp (SAC)\)

Mà \(BD \subset (SBD)\) suy ra \((SAC)\perp (SBD)\) (đpcm)

Câu b:

Vì ABCD la hình thoi cạnh a và \(\widehat{A}=60^0\)

\(\Rightarrow \widehat{C}=60^0; \widehat{B}=\widehat{D}=120^0\)

\(\Rightarrow AC^2=BC^2+BA^2-2BC.BA.cos120^0\)

\(=2a^2+a^2=3a^2\)

\(\Rightarrow AC=a\sqrt{3}\)

Trong tam giác vuông CSA có:

\(SA^2=SC^2+CA^2=\frac{6a^2}{4}+3a^2=\frac{18a^2}{4}\)

\(\Rightarrow SA=\frac{3a\sqrt{2}}{2}\)

Vì \(\Delta AIK\sim \Delta ASC \ (g.g)\)

\(\Rightarrow \frac{AI}{AS}=\frac{IK}{SC} \Rightarrow IK= \frac{AI.SC}{AS}= \frac{\frac{a\sqrt{3}}{2}. \frac{a\sqrt{6}}{2}}{\frac{3a\sqrt{2}}{2}}=\frac{a}{2}\)

Vậy \(IK=\frac{a}{2}\)

Câu c:

Vì \(\widehat{A}=60^0\) và \(AB=AD=a\Rightarrow \Delta ABD \ deu \ \Rightarrow BD=a\)

Tam giác KBD có \(KI=IB=ID=\frac{a}{2}\Rightarrow \Delta KBD\) vuông tại K hay \(\widehat{BKD}=60^0.\)

Nhận xét \(BD\perp (SAC)\) mà \(SA \subset (SAC) \Rightarrow BD \bot SA\)

Hơn nữa \(IK\perp SA\) suy ra \(SA\perp (KBD)\)

Mà SA là giao tuyến của (SAB) và (SAD) suy ra góc BKD chính là góc giữa mặt phẳng SAB và mặt phẳng (SAD)

Vậy \((SAB)\perp (SAD)\) (đpcm).

-- Mod Toán 11