Bài tập 4 trang 126 SGK Hình học 11

Bài tập 4 trang 126 SGK Hình học 11

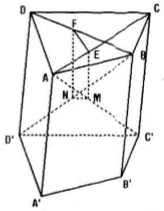
Nhận thấy: E, M lần lượt là trung điểm của AC và AC' ⇒ EM là đường trung bình của tam giác \(ACC'\Rightarrow EM=\frac{1}{2}CC'\) và EM // CC' (1).

Tương tự: FN cũng là đường trung điểm của tam giác BDD'.

\(\Rightarrow FN=\frac{1}{2}DD'\) và FN // DD' (2)

Từ (1), (2) và DD' // CC', DD'= CC'

Suy ra EM = FN và EM // FN

⇒ EFNM là hình bình hành

⇒ EF = MN (đpcm).

-- Mod Toán 11