Bài tập 5 trang 119 SGK Hình học 11

Bài tập 5 trang 119 SGK Hình học 11

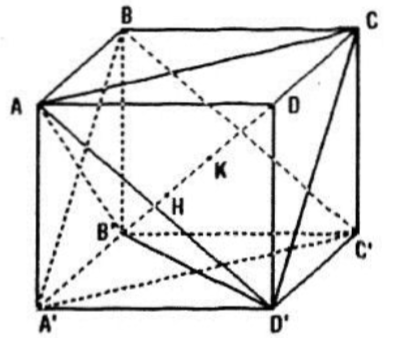
Câu a:

Vì ABB'A' là hình vuông nên \(A'B\perp AB'\) lại thấy \(AD\perp (ABB'A')\Rightarrow AD\perp A'B\) suy ra \(A'B\perp (ADB')\Rightarrow A'B\perp DB' \ (1)\)

Do A'B'C'D' là hình vuông \(\Rightarrow A'C'\perp B'D', DD'\perp (A'B'C'D')\Rightarrow DD'\perp A'C'\)

Suy ra \(A'C'\perp (DB'D')\Rightarrow A'C'\perp B'D \ (2)\)

Từ (1) và (2) suy ra \(B'D\perp (A'C'B)\)

Câu b:

Gọi H và K lần lượt là giao điểm của B'D với mặt phẳng (BA'C') và mặt phẳng (ACD')

Ta đã chứng minh được \(B'D\perp (BA'C')\) và \((BA'C') //(ACD')\Rightarrow DK\perp (ACD')\) và \(B'H\perp (BA'C')\)

Dễ thấy \(AC=AD'=CD'=a\sqrt{2}\) (giả sử cạnh của hình lập phường là a) và \(DK\perp (ACD')\Rightarrow \frac{1}{DK^2}= \frac{1}{DA^2}+\frac{1}{DC^2}+\frac{1}{DD^2}\)

\(\Rightarrow \frac{1}{DK^2}=\frac{1}{a^2}+\frac{1}{a^2}+\frac{1}{a^2}=\frac{3}{a^2}\)

\(\Rightarrow DK=\frac{a\sqrt{3}}{3}\)

Tương tự ta cũng có \(B'H=\frac{a\sqrt{3}}{3}\)

Mà \(B'D=a\sqrt{3}\Rightarrow HK=B'D-B'F-DK\)

\(=a\sqrt{3}-\frac{a\sqrt{3}}{3}- \frac{a\sqrt{3}}{3}=\frac{a\sqrt{3}}{3}\)

Vậy khoảng cách giữa hai mặt phẳng (ACD') và (BA'C') bằng \(HK=\frac{a\sqrt{3}}{3}\).

Câu c:

Vì \(BC'\subset (BA'C')\) bằng \(CD'\subset (BA'C')\), bên cạnh đó (ACD') // (BA'C') suy ra khoảng cách từ BC' đến CD' bằng khoảng cách giữa (ACD') và (BA'C') và bằng \(\frac{a\sqrt{3}}{3}.\)

-- Mod Toán 11