Bài tập 5 trang 98 SGK Hình học 11

Bài tập 5 trang 98 SGK Hình học 11

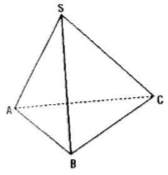
* Chứng minh \(SA\perp BC:\)

Xét tích vô hướng 

\(=\overrightarrow{SA}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB}\)

\(=\left |\overrightarrow{SA} \right |.\left |\overrightarrow{SC} \right | .cos(\overrightarrow{SA}.\overrightarrow{SC})- \left |\overrightarrow{SA} \right |.\left |\overrightarrow{SB} \right | .cos(\overrightarrow{SA}.\overrightarrow{SB})\)

\(=SA^2.cosASC -SA^2.cosBSA=\vec{0}\)

\(\Rightarrow SA\perp BC\) (đpcm)

* Chứng minh hoàn toàn tương tự ta cũng có:

\(SB\perp AC\) và \(SC\perp AB\)

-- Mod Toán 11

Video hướng dẫn giải bài 5 SGK