Bài tập 19 trang 103 SGK Hình học 11 NC
Bài tập 19 trang 103 SGK Hình học 11 NC
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm tam giác ABC.
a. Chứng minh rằng SG ⊥ (ABC). Tính SG.
b. Xét mặt phẳng (P) đi qua A và vuông góc với đường thẳng SC. Tìm hệ thức liên hệ giữa a và b để (P) cắt SC tại điểm C1 nằm giữa S và C. Khi đó hãy tính diện tích thiết diện của hình chóp S.ABC khi cắt bởi mp(P).
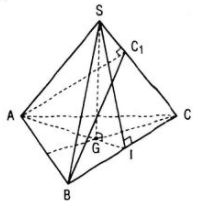
a) Vì SA = SB = SC nên S nằm trên trục của đường tròn ngoại tiếp tam giác ABC.
Mà G là tâm đường tròn ngoại tiếp tam giác ABC nên SG ⊥ mp(ABC)
Gọi I là trung điểm của BC.
Ta có : AI ⊥ BC và BC ⊥ SI
\(\begin{array}{*{20}{l}}
\begin{array}{l}
SI = \sqrt {S{C^2} - I{C^2}} \\
= \sqrt {{b^2} - \frac{{{a^2}}}{4}} = \sqrt {\frac{{4{b^2} - {a^2}}}{2}}
\end{array}\\
{GI = \frac{1}{3}AI = \frac{1}{3}.a\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}}
\end{array}\)
Trong tam giác vuông SGI ta có :
\(\begin{array}{*{20}{l}}
\begin{array}{l}
SG = \sqrt {S{I^2} - G{I^2}} \\
= \sqrt {\frac{{4{b^2} - {a^2}}}{4} - \frac{{{a^2}}}{{12}}}
\end{array}\\
{ = \sqrt {\frac{{12{b^2} - 4{a^2}}}{{12}}} = \sqrt {\frac{{3{b^2} - {a^2}}}{3}} }
\end{array}\)
b) Kẻ AC1 ⊥ SC thì (P) chính là mp(ABC1)
Vì SAC là tam giác cân mà AC1 ⊥ SC nên C1 nằm giữa S và C khi và chỉ khi
\(\begin{array}{l}
\widehat {ASC} < {90^0}\\
\Leftrightarrow A{S^2} + C{S^2} > A{C^2}\\
\Leftrightarrow 2{b^2} > {a^2}
\end{array}\)
Ta có : AB ⊥ GC và AB ⊥ SG ⇒ AB ⊥ SC
SC ⊥ AC1 và SC ⊥ AB nên SC ⊥ (ABC1)
Thể tích tứ diện SABC là:
\(\begin{array}{*{20}{l}}
{{V_{SABC}} = \frac{1}{3}SG.{S_{ABC}} = \frac{1}{3}SC.{S_{AB{C_1}}}}\\
\begin{array}{l}
\Rightarrow {S_{AB{C_1}}} = \frac{{SG.{S_{ABC}}}}{{SC}}\\
= \frac{{\sqrt {\frac{{3{b^2} - {a^2}}}{3}} .\frac{{{a^2}\sqrt 3 }}{4}}}{b} = \frac{{{a^2}\sqrt {3{b^2} - {a^2}} }}{{4b}}
\end{array}
\end{array}\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
