Bài tập 5 trang 92 SGK Hình học 11

Bài tập 5 trang 92 SGK Hình học 11

Ta dựng hình hộp dựa trên ba vecto \(\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\) (đây là các vecto không đồng phẳng). Hình a, kí hiệu ABMC.DNEP.

Câu a:

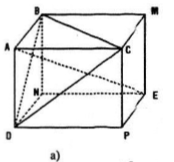
Khi đó: \(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}= \overrightarrow{AE}\) với điểm E là đỉnh của hình hộp và AE là đường chép của hình hộp đó.

Câu b:

\(\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AD}= \overrightarrow{AM}-\overrightarrow{AD}=\overrightarrow{DM}\)

\(\Rightarrow \overrightarrow{AF}=\overrightarrow{DM}\Rightarrow AFMD\) là hình bình hành (hình b)

Gọi I là trung điểm của AM, trong mặt phẳng (AMD) dựng DI cắt ME kéo dài F, đây chính là điểm cần xác định.

-- Mod Toán 11

Video hướng dẫn giải SGK