Bài tập 8 trang 98 SGK Hình học 11
Bài tập 8 trang 98 SGK Hình học 11
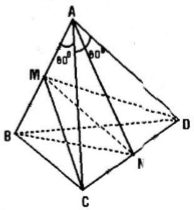
Cho tứ diện ABCD có AB = AC = AD và \(\widehat{BAC}=\widehat{BAD}=60^{0}.\) Chứng minh rằng:
a) AB ⊥ CD;
b) Nếu M, N lần lượt là trung điểm của AB và CD thì MN ⊥ AB và MN ⊥ CD.
Câu a:
Xét tích vô hướng:
\(\overrightarrow{AB}.\overrightarrow{CD}= \overrightarrow{AB}.(\overrightarrow{AD}-\overrightarrow{AC})\)
\(=\overrightarrow{AB}.\overrightarrow{AD}- \overrightarrow{AB}.\overrightarrow{AC}\)
\(=\left |\overrightarrow{AB} \right |.\left |\overrightarrow{AD} \right |.cos\widehat{BAD} - \left |\overrightarrow{AB} \right |.\left |\overrightarrow{AC} \right |.cos \widehat{BAC}\)
\(=AB.AD.cos60^0-AB.AC.cos60^0 =0\) (Vì AB = AC = AD)
\(\Rightarrow AB\perp CD\) (đpcm).
Câu b:
Nhận thấy: tam giá ABC có AB = AC và \(\widehat{BAC}=60^0\Rightarrow\) tam giác ABC là tam giác đều ⇒ AB = BC = AC.
Tương tự cũng có tam giác ABD đều ⇒ AB = AD = BD.
\(\Rightarrow \Delta ACD=\Delta BCD\) (c.c.c) ⇒ các trung tuyến BN và AN bằng nhau.
\(\Rightarrow \Delta NAB\) cần đỉnh N mà M là tam giác cân đỉnh M mà N là trung điểm CD \(\Rightarrow MN\perp CD\)
Vậy \(MN\perp AB\) và \(MN\perp CD\) (đpcm).
-- Mod Toán 11
Video hướng dẫn giải bài 8 SGK
Copyright © 2021 HOCTAP247
