Bài tập 1 trang 97 SGK Hình học 11
Bài tập 1 trang 97 SGK Hình học 11
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây:
a) \(\overrightarrow{AB}\) và \(\overrightarrow{EG};\) b) và
c)
và
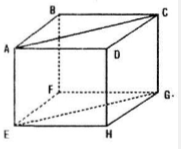
Câu a:
Ta có: \(\overrightarrow{EG}=\overrightarrow{AC}\)
\(\Rightarrow (\overrightarrow{AB}, \overrightarrow{EG})= (\overrightarrow{AF},\overrightarrow{AC})=45^0\)
Câu b:
Ta có: \((\overrightarrow{AF},\overrightarrow{EG})= (\overrightarrow{AF},\overrightarrow{AC})=\overrightarrow{CAF}\)
Vì AC, AF, FC là đường chéo của các hình vuông bằng nhau nên AC = AF = FC.
\(\Rightarrow \Delta AFC\) đều \(\Delta \widehat{CAF}=60^0\)
Vậy \((AF,EG)=60^0\)
Câu c:
Ta có: \((\overrightarrow{AB}, \overrightarrow{DH})= (\overrightarrow{AB}, \overrightarrow{BF})=90^0\)
-- Mod Toán 11
Video hướng dẫn giải bài 1 SGK
Copyright © 2021 HOCTAP247
