Bài tập 8 trang 105 SGK Hình học 11
Bài tập 8 trang 105 SGK Hình học 11
Cho điểm S không thuộc cùng mặt phẳng (α) có hình chiếu là điểm H. Với điểm M bất kì trên (α) và M không trùng với H, ta gọi SM là đường xiên và đoạn HM là hình chiếu của đường xiên đó. Chứng minh rằng:
a) Hai đường thẳng xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau;
b) Với hai đường xiên cho trước, đường xiên nào lớn hơn thì có hình chiếu lớn hơn và ngược lại đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
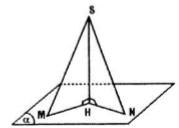
Lấy điểm \(N\not\equiv M\) trên \((\alpha )\)
Câu a:
Giả sử: \(HM=HN\)
Ta thấy tam giác HSM và tam giác HSN có:
HS chung; \(HM=HN; \widehat{SHM}=\widehat{SHN}=90^0\)
Ngược lại nếu SM = SN thì hai tam giác vuông HSM và HSN cũng bằng nhau.
⇒ HM = HN
Vậy HM = HN ⇔ SM = SN (đpcm)
Câu b:
Giả sử \(HM >HN \Leftrightarrow \sqrt{SM^2-SH^2}>\sqrt{SN^2-SH^2}\)
\(\Leftrightarrow SM^2>SN^2\)
\(\Leftrightarrow SM>SN\) (đpcm)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
