Bài tập 1 trang 120 SGK Hình học 11 NC

Bài tập 1 trang 120 SGK Hình học 11 NC

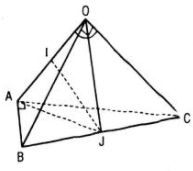
a) Vì \(\widehat {AOB} = \widehat {AOC} = {60^0}\)

OA = OB = OC = a

Nên AB = AC = a

Suy ra ΔABC = ΔOBC

Vậy tam giác ABC vuông cân tại A

Gọi J là trung điểm của BC thì OJ ⊥ BC, AJ ⊥ BC nên OA ⊥ BC.

b) Gọi I là trung điểm của OA, do OJ = AJ nên JI ⊥ OA, mà JI ⊥ BC, vậy IJ là đường vuông góc chung của OA và BC.

\(\begin{array}{l}
I{J^2} = O{J^2} - O{I^2}\\
 = {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{{a^2}}}{4}
\end{array}\)

\(\begin{array}{*{20}{l}}
\begin{array}{l}
I{J^2} = O{J^2} - O{I^2}\\
 = {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{{a^2}}}{4}
\end{array}\\
{ \Rightarrow d\left( {OA;BC} \right)\frac{a}{2}}
\end{array}\)

c) Từ các kết quả trên ta có :

OJ ⊥ BC, AJ ⊥ BC, IJ = \(\frac{1}{2}OA\)

Vậy góc giữa mp(OBC) và mp(ABC) bằng góc \(\widehat {OJA}\) và \(\widehat {OJA} = {90^0}\), do đó mp(OBC) ⊥ mp(ABC).

-- Mod Toán 11