Bài tập 4 trang 121 SGK Hình học 11

Bài tập 4 trang 121 SGK Hình học 11

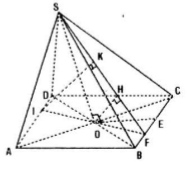
Câu a:

Vì E là trung điểm BC và O là trung điểm AC.

\(\Rightarrow OE=\frac{1}{2}AB=\frac{a}{2}\)

Do ABCD là hình thoi nên góc \(\widehat {BAD} = {60^0}.\)

\(\Rightarrow \Delta BAD\) đều \(\Rightarrow BD=a\Rightarrow OB=\frac{a}{2}\)

\(\Rightarrow \Delta OBE\) làm tam giác đều.

F là trung điểm \(BE\Rightarrow OF\perp BE\Rightarrow OF\perp BC\) (1)

Lại có \(SO \perp (ABCD)\Rightarrow SO\perp BC\) (2)

Từ (1) và (2) suy ra \(BC\perp (SOF)\)

Mà \(BC\subset (SBC)\Rightarrow (SOF )\perp (SBC)\) (đpcm).

Câu b:

Trong mặt phẳng (SOF) và \(OH\perp SF(H\in SF)\)

vì \(BC\perp (SOF)\Rightarrow BC\perp OH\Rightarrow OH\perp (SBC)\)

⇒ độ dài đoạn thẳng OH là khoảng cách từ O đến mặt phẳng (SBC).

Trong tam giác vuông OSF có đường cao \(OH\Rightarrow \frac{1}{OH^2}=\frac{1}{OS^2}+\frac{1}{OF^2}\)

\(\Rightarrow \frac{1}{OH^2} = \frac{1}{\frac{9a^2}{16}}+\frac{1}{\frac{3a^2}{16}}= \frac{64}{9a^2}\Rightarrow OH=\frac{3a}{8}\)

Gọi I là giao điểm của OF và AD. Trong mặt phẳng (SIF) dựng \(IK\perp SF\)

Vì \(OH\perp SF, IK\perp SF\Rightarrow OH // IK\Rightarrow IK\perp (SBC)\)

⇒ độ dài đoạn thẳng IK là khoảng cách từ I đến mặt phẳng (SBC)

Lại thấy \(I\in AD\) mà AD // (SBC) ⇒ IK là khoảng csch từ AD đến mặt phẳng (SBC) hay IK là khoảng cách từ A đến mặt phẳng (SBC).

Dễ thấy OH là đường trung bình của \(\Delta FIK\)

\(\Rightarrow IK=3.OH=\frac{3a}{4}\)

Vậy \(d(O,(SBC))=\frac{3a}{8}\) và \(d(A,(SBC))=\frac{3a}{4}\).

-- Mod Toán 11