Bài tập 9 trang 92 SGK Hình học 11
Bài tập 9 trang 92 SGK Hình học 11
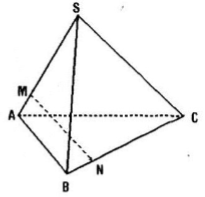
Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho \(\overrightarrow{MS}\) = \(-2\overrightarrow{MA}\) và trên đoạn BC lấy điểm N sao cho \(\overrightarrow{NB}=-\frac{1}{2}\overrightarrow{NC}.\) Chứng minh rằng ba véctơ \(\overrightarrow{AB}\), \(\overrightarrow{MN}\), \(\overrightarrow{SC}\) đồng phẳng.
\(\overrightarrow{MN}= \overrightarrow{MA} + \overrightarrow{AB} + \overrightarrow{BN}\)
\(\overrightarrow{MN}= \overrightarrow{MS} + \overrightarrow{SC} + \overrightarrow{CN}\)
\(\Rightarrow 2\overrightarrow{MN}= (\overrightarrow{MA}+\overrightarrow{MS})+ (\overrightarrow{AB}+\overrightarrow{SC})+ (\overrightarrow{BN}+\overrightarrow{CN})\)
\(=-\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{SC}- \overrightarrow{BN}\)
\(=-(\overrightarrow{MA}+\overrightarrow{BN})+\overrightarrow{AB}+ \overrightarrow{SC}\)
\(=-(\overrightarrow{MN}+\overrightarrow{AB})+\overrightarrow{AB}+ \overrightarrow{SC}\)
\(\Rightarrow 3\overrightarrow{MN}=2\overrightarrow{AB}+ \overrightarrow{SC}\Rightarrow \overrightarrow{MN}=\frac{2}{3}\overrightarrow{AB}+ \frac{1}{3}\overrightarrow{SC}.\)
⇒ Các vecto \(\overrightarrow{MN}, \overrightarrow{AB}, \overrightarrow{SC}\) đồng phẳng (đpcm).
-- Mod Toán 11
Video hướng dẫn giải SGK
Copyright © 2021 HOCTAP247
