Bài tập 7 trang 92 SGK Hình học 11
Bài tập 7 trang 92 SGK Hình học 11
Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh rằng:
a) \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\)
b) \(\overrightarrow{PI}=\frac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD})\)
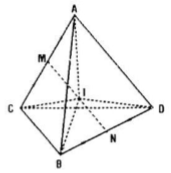
Câu a:
\(\overrightarrow{IA}+\overrightarrow{IC}=2\overrightarrow{IM},\)
\(\overrightarrow{IB}+\overrightarrow{ID}=2\overrightarrow{IN}.\)
\(\overrightarrow{IA}+\overrightarrow{IC}+\overrightarrow{IB}+\overrightarrow{ID} =2(\overrightarrow{IM}+\overrightarrow{IN})=\overrightarrow{0}\)
Câu b:
\(\Rightarrow 4\overrightarrow{PI}= \overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+ \overrightarrow{PD}+\overrightarrow{AI}+\overrightarrow{BI} +\overrightarrow{CI}+\overrightarrow{DI}\)
\(=\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+ \overrightarrow{PD}+\overrightarrow{0}\)
\(4\overrightarrow{PI}=\frac{1}{4}(\overrightarrow{PA}+ \overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD})\) (đpcm)
-- Mod Toán 11
Video hướng dẫn giải SGK
Copyright © 2021 HOCTAP247
