Bài tập 4 trang 91 SGK Hình học 11 NC
Bài tập 4 trang 91 SGK Hình học 11 NC
Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của các tứ diện A’D’MN và BCC’D’. Chứng minh rằng đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
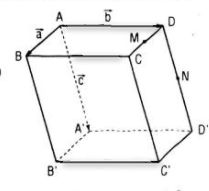
Đặt \(\overrightarrow {AB} = \overrightarrow a ;\overrightarrow {AD} = \overrightarrow b ;\overrightarrow {AA'} = \overrightarrow c \)
Vì G là trọng tâm tứ diện BCC'D nên ta có:
\(\overrightarrow {AG'} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AC'} + \overrightarrow {AD'} } \right)\)
Và G là trọng tâm tứ diện A’D’MN nên
\(\begin{array}{l}
\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow {AA'} + \overrightarrow {AD'} + \overrightarrow {AM} + \overrightarrow {AN} } \right)\\
\Rightarrow \overrightarrow {GG'} = \overrightarrow {AG'} - \overrightarrow {AC} \\
= \frac{1}{4}\left( {\overrightarrow {A'B} + \overrightarrow {D'C} + \overrightarrow {MC'} + \overrightarrow {ND'} } \right)\\
= \frac{1}{4}\left( {\overrightarrow a - \overrightarrow c + \overrightarrow a - \overrightarrow c + \frac{1}{2}\overrightarrow a + \overrightarrow c + \frac{1}{2}\overrightarrow c } \right)\\
= \frac{1}{8}\left( {5\overrightarrow a - \overrightarrow c } \right) = \frac{1}{8}\left( {5\overrightarrow {AB} - \overrightarrow {AA'} } \right)
\end{array}\)
Do đó \(\overrightarrow {AB} ,\overrightarrow {AA'} ,\overrightarrow {GG'} \) đồng phẳng.
Mặt khác, G không thuộc mặt phẳng (ABB’A’) nên đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
