Bài tập 10 trang 92 SGK Hình học 11

Bài tập 10 trang 92 SGK Hình học 11

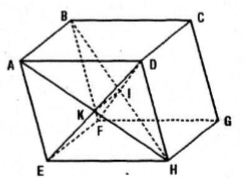
Nhận thấy K và I lần lượt là trung điểm của AH và BH.

⇒ KI là đường trung bình của tam giác HAB.

⇒ KI // AB ⇒ giá của vecto \(\overrightarrow{KI}\) song song với mặt phẳng (ABCD)

Mặt khác \(\overrightarrow{FG}=\overrightarrow{BC}\Rightarrow\) giá của vecto \(\overrightarrow{FG}\) cũng song song với mặt phẳng (ABCD). Còn vecto \(\overrightarrow{AC}\) có giá nằm trên mặt phẳng (ABCD).

Vậy các vecto \(\overrightarrow{AC},\overrightarrow{KI},\overrightarrow{FG}\) đồng phẳng (đpcm).

-- Mod Toán 11

Video hướng dẫn giải bài 1 SGK