Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
Bài tập 8 trang 92 SGK Hình học 11
Bài tập 8 trang 92 SGK Hình học 11
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 8 trang 92 SGK Hình học 11
Cho hình lăng trụ tam giác ABC.A'B'C' có \(\overrightarrow{AA}\) = \(\overrightarrow{a}\), \(\overrightarrow{AB}\) = \(\overrightarrow{b}\), \(\overrightarrow{AC}\) = \(\overrightarrow{c}\). Hãy phân tích (hay biểu thị véctơ \(\overrightarrow{B'C}\), \(\overrightarrow{BC'}\) qua các véctơ \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\).
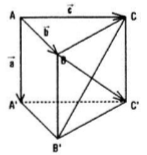
Ta có:
\(\overrightarrow{B'C}= \overrightarrow{B'B}+\overrightarrow{BC}= \overrightarrow{B'B}+\overrightarrow{AC}-\overrightarrow{AB}\)
\(=-\vec{a}+\vec{c}-\vec{b}\)
\(\overrightarrow{BC'}=\overrightarrow{BC}+\overrightarrow{BB'}= \overrightarrow{AC}-\overrightarrow{AB}+\overrightarrow{BB'}\)
\(=\vec{c}-\vec{b}+\vec{a}\)
-- Mod Toán 11
Video hướng dẫn giải SGK
Copyright © 2021 HOCTAP247
