Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
Bài tập 3 trang 104 SGK Hình học 11
Bài tập 3 trang 104 SGK Hình học 11
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 3 trang 104 SGK Hình học 11
Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SB = SC = SD. Chứng minh rằng:
a) Đường thẳng SO vuông góc với mặt phẳng (ABCD)
b) Đường thẳng AC vuông góc với mặt phẳng (SBD) và đường thẳng BD vuông góc với mặt phẳng (SAC)
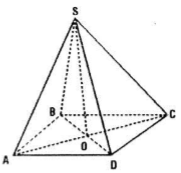
Câu a:
Vì SA = SC ⇒ tam giác SAC cân đỉnh S, mặt khác O là trung điểm của AC
\(\Rightarrow SO\perp AC\)
Tương tự \(SO\perp BD\)
Suy ra \(SO\perp (ABCD)\) (đpcm)
Câu b:
* Ta có \(SO\perp AC\) và \(BD\perp AC\) (hai đường chéo của hình thoi)
\(\Rightarrow AC\perp (ABD)\)
+ \(AC\perp BD\) (đường chéo hình thoi)
+ \(AC\perp SO\)
+ BD cắt SO trong (SBD)
* Ta có:
+ \(BD\perp AC\)
+\(BD\perp SO\)
+ AC cắt SO trong (SAC)
\(\Rightarrow BD\perp (SAC)\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
