Bài tập 7 trang 114 SGK Hình học 11
Bài tập 7 trang 114 SGK Hình học 11
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, CC' = c.
a) Chứng minh rằng mặt phẳng (ADC'B') vuông góc với mặt phẳng (ABB'A').
b) Tính độ dài đường chéo AC' theo a, b, c.
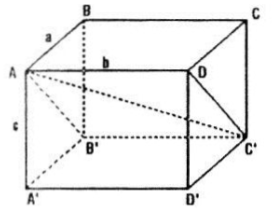
Câu a:
Vì ABCD là hình chữ nhật nên \(AD\perp AB \(1)\) vì ADD'A' là hình chữ nhật nên \(AD\perp AA' \ (2)\) từ (1) và (2) \(\Rightarrow AD\perp (ABB'A')\) mà \(AD\subset (ADC'B')\) nên \((ADC'B')\perp (ABB'A')\).
Câu b:
Ta có: \(\overrightarrow{AC'}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}\)
\(\Rightarrow \overrightarrow{AC'}^2= (\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'})^2\)
\(=\overrightarrow{AB}^2+\overrightarrow{AD}^2+\overrightarrow{AA'}^2+ 2(\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AB}.\overrightarrow{AA'} +\overrightarrow{AA'}.\overrightarrow{AD})\)
\(=a^2+b^2+c^2\)
(vì \(AB\perp AD,AB\perp AA', AD\perp AA'\) nên các tích vô hướng \(\overrightarrow{AB}.\overrightarrow{AD}=0,\overrightarrow{AB}. \overrightarrow{AA'}=0, \overrightarrow{AD}.\overrightarrow{AA'}=0\))
Vậy \(AC'=\sqrt{a^2+b^2+c^2}\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
