Bài tập 2 trang 119 SGK Hình học 11
Bài tập 2 trang 119 SGK Hình học 11
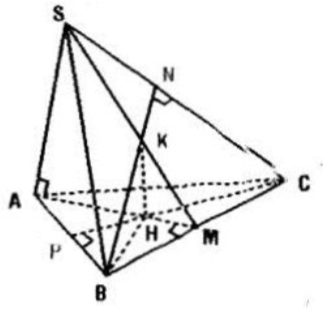
Cho tứ diện S.ABC có SA vuông góc với mặt phẳng (ABC). Gọi H, K lần lượt là trực tâm của tam giác ABC và SBC.
a) Chứng minh ba đường thẳng AH, SK, BC đồng quy.
b) Chứng minh rằng SC vuông góc với mặt phẳng (BHK) và HK vuông góc với mặt phẳng (SBC).
c) Xác định đường vuông góc chung của BC và SA
Câu a:
Gọi M là chân đường cao hạ từ S xuống BC vì \(SA\perp (ABC)\Rightarrow AM\) là hình chiếu vuông góc của SM trên mặt phẳng (ABC).
Vì \(SM\perp BC\Rightarrow AM\perp BC\) (theo định lí ba đường vuông góc)
Vì H, K là trực tâm của \(\Delta ABC, \Delta SBC\) nên AH, SK và BC đồng quy tại M (đpcm).
Câu b:
Vì H là trực tâm của tam giác \(ABC\Rightarrow BH\perp AC \ (1)\)
Vì \(SA\perp (ABC);BH\subset (SAC)\Rightarrow BH\perp SA \ (2)\)
Từ (1) và (2) suy ra \(BH \perp (SAC)\Rightarrow BH\perp SC \ (3)\)
Vì K là trực tâm của \(\Delta SBC\Rightarrow BK\perp SC \ (4)\)
Từ (3) và (4) suy ra \(SC\perp (BHK)\) (đpcm)
Theo chứng minh trên \(SC\perp (BHK)\Rightarrow HK\perp SC \ (5)\)
Mặt khác do \(AM\perp BC\) và \(SM\perp BC\Rightarrow BC\perp (ASM)\Rightarrow BC\perp HK \ (6)\)
Từ (5) và (6) suy ra \(HK\perp (SBC)\) (đpcm)
Câu c:
Ta có AM \( \bot \) BC tại M. Do SA \( \bot \) (ABC) nên AM \( \bot \) SA tại A.
Suy ra AM là đường vuông góc chung của BC và SA.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
