Bài tập 9 trang 114 SGK Hình học 11

Bài tập 9 trang 114 SGK Hình học 11

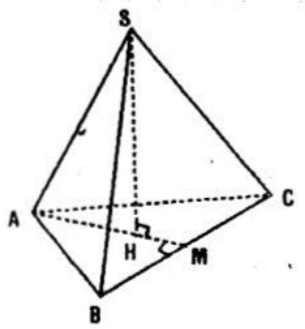
Gọi M là trung điểm \(BC\Rightarrow AM\perp BC (1)\)

Vì SH là đường cao của hình chóp nên \(SH\perp (ABC)\)

Và \(H\in (ABC)\)

Vì S.ABC là hình chóp đều

⇒ SA = SB = SC

⇒ HA = HB = HC ⇒ H là tâm đường tròn ngoại tiếp tam giác đều ABC.

\(\Rightarrow H\in AM\)

⇒ HA là hình chiếu của SA trên mặt phẳn (ABC) (2)

Từ (1), (2) và theo định lý ba đường vuông góc suy ra \(SA\perp BC\)

Tương tự ta chứng minh được \(SB\perp AC\) (và \(SC\perp AB\))

-- Mod Toán 11