Bài tập 4 trang 105 SGK Hình học 11
Bài tập 4 trang 105 SGK Hình học 11
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng:
a) H là trực tâm của tam giác ABC;
b) \(\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OB^{2}}+\frac{1}{OC^{2}}.\)
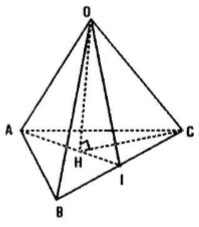
Câu a:
Dễ thấy AH là hình chiếu vuông góc của AO trên mặt phẳng (ABC), vì:
\(\left.\begin{matrix} OA\perp OB\\ OA\perp OC \end{matrix}\right\}\Rightarrow OA\perp (OBC)\)
\(\Rightarrow OA\perp BC'\)
Theo định lý ba đường vuông góc suy ra \(AH\perp BC\)
Tương tự ta cũng có \(CH\perp AB\)
⇒ H là trực tâm của tam giác ABC (đpcm)
Câu b:
Gọi I là giao điểm của AH và BC.
\(\Rightarrow BC\perp AI\)
Mặt khác \(OA\perp BC\) suy ra \(BC\perp (OAI)\Rightarrow BC\perp OI\)
Trong tam giác vuông OAI có đường cao \(OH\Rightarrow \frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OI^2}\)
Trong tam giác vuông OBC có đường cao \(OI\Rightarrow \frac{1}{OI^2}=\frac{1}{OB^2}+\frac{1}{OC^2}\)
Vậy \(\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OB^{2}}+\frac{1}{OC^{2}}.\) (đpcm)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
