Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
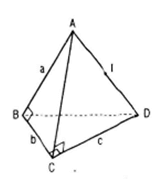
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc và AB = a, BC = b, CD = c.
a. Tính độ dài AD.
b. Chỉ ra điểm cách đều A, B, C, D
c. Tính góc giữa đường thẳng AD và mặt phẳng (BCD), góc giữa đường thẳng AD và mặt phẳng (ABC).
a) Ta có: CD ⊥ BC và CD ⊥ AB nên CD ⊥ (ABC)
mà AC ⊂ (ABC) do đó CD ⊥ AC.
Trong tam giác vuông ABC ta có:
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2}\)
Trong tam giác vuông ACD ta có:
\(\begin{array}{l}
A{D^2} = A{C^2} + C{D^2} = {a^2} + {b^2} + {c^2}\\
\Rightarrow AD = \sqrt {{a^2} + {b^2} + {c^2}}
\end{array}\)
b) Ta có: AB ⊥ BC và AB ⊥ CD suy ra AB ⊥ (BCD) do đó AB ⊥ BD.
Gọi I là trung điểm AD ta có IC = IA = IB = ID.
Vậy I cách đều A, B, C, D.
c) Ta có: AB ⊥ (BCD) ⇒ BD là hình chiếu của ADAD trên (BCD)
Khi đó:
\(\widehat {\left( {AD,\left( {BCD} \right)} \right)} = \widehat {\left( {AD,BD} \right)} = \widehat {ADB}\)
Xét tam giác ABD vuông tại B thì
\(\sin \widehat {ADB} = \frac{{AB}}{{AD}} = \frac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
\( \Rightarrow \widehat {(AD,(BCD))} = arcsin\frac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Lại có DC ⊥ (ABC) ⇒ AC là hình chiếu của AD trên (ABC)
Khi đó
\(\widehat {\left( {AD,\left( {ABC} \right)} \right)} = \widehat {\left( {AD,AC} \right)} = \widehat {DAC}\)
Xét tam giác ACD vuông tại C thì
\(\sin \widehat {DAC} = \frac{{CD}}{{AD}} = \frac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
\( \Rightarrow \widehat {(AD,(ABC))} = arcsin\frac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247