Bài tập 3 trang 119 SGK Hình học 11

Bài tập 3 trang 119 SGK Hình học 11

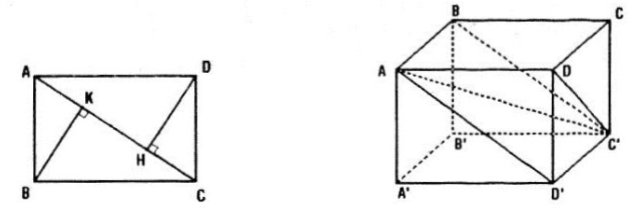
Vì ABCD.A'B'C'D' là hình lập phương ⇒ các tứ giác ABC'D', ACC'A', ADC'B' là các hình chữ nhật bằng nhau và có chung đường chéo AC'. Suy ra khoảng cách từ các điểm B, C, D, A', B', D' đến đường chéo AC' bằng nhau.

Ta chỉ tính một khoảng cách rồi suy ra kết quả còn lại.

Xét hình chữ nhật ABC'D' có các cạnh

\(AD'=a\sqrt{2}; AB=a\Rightarrow AC'=a\sqrt{3}.\)

Gọi K, H lần lượt là chân đường vuông góc hạ từ B và D' xuống AC'

⇒ BK = D'H là khoảng cách từ B và D' đến AC'.

Dễ thấy \(\Delta ABK\sim \Delta AC'B \ (g.g)\Rightarrow \frac{AB}{AC'}=\frac{BK}{C'B}\Rightarrow BK= \frac{AB.C'B}{AC'}\)

\(\Rightarrow BK=\frac{a.a\sqrt{2}}{a\sqrt{3}}=\frac{a\sqrt{6}}{3}\)

Vậy khoảng cách từ các điểm B, C, D, A', B', D' đến AC' bằng nhau và bằng \(\frac{a\sqrt{6}}{3}\).

-- Mod Toán 11