Bài tập 3 trang 121 SGK Hình học 11
Bài tập 3 trang 121 SGK Hình học 11
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).
a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng (\(\alpha\)) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, AC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB.
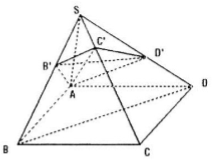
Câu a:
Do \(SA \bot (ABCD) \Rightarrow SA \bot AB\) và \(SA \bot AD.\)
Nên các tam giác SAB và SAD là các tam giác vuông tại A.
Do \(\left\{ \begin{array}{l} BC \bot SA\\ BC \bot AB \end{array} \right. \Rightarrow BC \bot (SAB)\Rightarrow BC \bot SB.\)
\(\Rightarrow \Delta SBC\) vuông tại B.
Do \(\left\{ \begin{array}{l} CD \bot AD\\ CD \bot SA \end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AD.\)
\(\Rightarrow \Delta SCD\) vuông tại D.
Vậy các mặt bên của hình chóp là các tam giác vuông.
Câu b:
Vì \(BD\perp AC\) và \(BD\perp SA\) nên \(BD\perp (SAC)\Rightarrow BD\perp SC\)
Mặc khác vì \(\left ( \alpha \right ) \bot SC\) nên \(B'D' \bot SC.\)
Hai đường thẳng BD và B'D' cùng nằm trong mặt phẳng (SBD) và cùng vuông góc với SC.
Vì SC không vuông góc với (SBD) nên hình chiếu của SC trên mặt phẳng (SBD) sẽ vuông góc với BD và B'D'.
Suy ra: BD//B'D'.
Ta có: \(\left. \begin{array}{l} BD \bot (SAB) \Rightarrow BC \bot AB'\\ SC \bot \left( \alpha \right) \Rightarrow SC \bot AB' \end{array} \right\} \Rightarrow AB' \bot (SBC) \Rightarrow AB' \bot SB.\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
