Bài tập 6 trang 119 SGK Hình học 11

Bài tập 6 trang 119 SGK Hình học 11

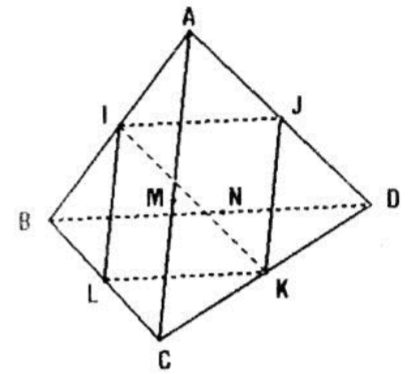
Gọi I, J, K, L, M, N lần lượt là trung điểm của AB, AD, CD, BC, AC, BD

Ta có: \(\left.\begin{matrix} IK\perp CD\\ IJ // CD \end{matrix}\right\} \Rightarrow IK \perp JM \ (1)\)

Và \(\left.\begin{matrix} IK\perp AB\\ JN // AB \end{matrix}\right\} \Rightarrow IK \perp JN \ (2)\)

Từ (1) và (2) suy ra \(IK \perp (JMLN)\)

\(\Rightarrow IK\perp JL\)

Mặt khác IJKL là hình bình hành

⇒ IJKL là hình thoi ⇒ IJ = JK

Mà BD = 2IJ; AC = 2JK ⇒ BD = AC.

Chứng minh tương tự ta cũng được: AD = BC.

Vậy AD = BC và BD = AC (đpcm).

-- Mod Toán 11