Bài tập 6 trang 105 SGK Hình học 11

Bài tập 6 trang 105 SGK Hình học 11

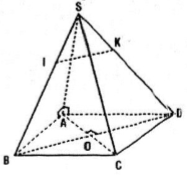
Câu a:

Ta thấy ABCD là hình thoi suy ra các đường chéo AC và BD vuông góc với nhau tại O hay \(BD\perp AC\) (1).

Mặt khác theo giả thiết \(SA\perp (ABCD)\)

\(\Rightarrow BD\perp SA (2)\)

Từ (1) và (2) suy ra \(BD\perp (SAC)\)  (3)

\(\Rightarrow BD\perp SC\) (đpcm)

Câu b:

Từ giả thiết \(\frac{SI}{SB}=\frac{SK}{SD}\Rightarrow IK // BD \ (4)\)

Từ (3) và (4) suy ra \(IK\perp (SAC)\) (đpcm)

-- Mod Toán 11