Bài tập 2 trang 91 SGK Hình học 11
Bài tập 2 trang 91 SGK Hình học 11
Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:
a) \(\overrightarrow{AB} + \overrightarrow{B'C'} + \overrightarrow{DD'} = \overrightarrow{AC'};\)
b) \(\overrightarrow{BD} - \overrightarrow{D'D} - \overrightarrow{B'D'} = \overrightarrow{BB'};\)
c) \(\overrightarrow{AC} + \overrightarrow{BA'} + \overrightarrow{DB} + \overrightarrow{C'D} = \overrightarrow{0}.\)
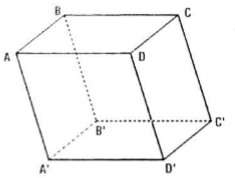
Câu a:
\(\overrightarrow{AB} + \overrightarrow{B'C'} + \overrightarrow{DD'} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA'} = \overrightarrow{AC'};\)
Câu b:
\(\overrightarrow{BD} - \overrightarrow{D'D} - \overrightarrow{B'D'} = \overrightarrow{BD} + \overrightarrow{DD'} + \overrightarrow{D'B'} = \overrightarrow{BB'};\)
Câu c:
\(\overrightarrow{AC} + \overrightarrow{BA'} + \overrightarrow{DB} + \overrightarrow{C'D}\)
\(=(\overrightarrow{AB}+\overrightarrow{AD})+ (\overrightarrow{BA}+\overrightarrow{BB})+ (\overrightarrow{DA}+\overrightarrow{DC})+ (\overrightarrow{C'C}+\overrightarrow{C'D})\)
\(=(\overrightarrow{AB}+\overrightarrow{BA})+ (\overrightarrow{AD}+\overrightarrow{DA})+ (\overrightarrow{BB'}+\overrightarrow{C'C})+ (\overrightarrow{DC}+\overrightarrow{C'D})\)
\(=\overrightarrow{0}\)
-- Mod Toán 11
Video hướng dẫn giải SGK
Copyright © 2021 HOCTAP247
