Bài tập 4 trang 114 SGK Hình học 11
Bài tập 4 trang 114 SGK Hình học 11
Cho hai mặt phẳng \((\alpha )\), \((\beta )\) cắt nhau và một điểm M không thuộc \((\alpha )\) và \((\beta )\). Chứng minh rằng qua điểm M có một và chỉ một mặt phẳng (P) vuông góc với \((\beta )\)và \((\beta )\). Nếu \((\alpha ) // (\beta )\) thì kết quả trên sẽ thay đổi như thế nào?
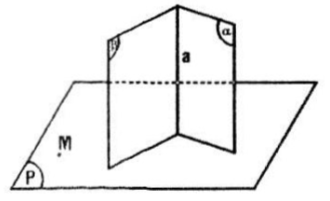
Ta có:
\(\left.\begin{matrix} (\alpha )\perp (P)\\ (\beta )\perp (P)\\ a=(\alpha )\cap (\beta ) \end{matrix}\right\}\Rightarrow a\perp (P)\)
Vì qua một điểm M cho trước có một và chỉ một mặt phẳng vuông góc với một đường thẳng cho trước nên qua M có một và chỉ một mặt phẳng (P) vuông góc với a.
Hay nói cách khác mặt phẳng (P) qua M vuông góc với \((\alpha )\) và \((\beta )\) là duy nhất.
* Nếu \((\alpha ) // (\beta )\) thì qua M có vô số mặt phẳng (P) vuông góc với cả \((\alpha )\) và \((\beta )\).
-- Mod Toán 11
Copyright © 2021 HOCTAP247
