Bài tập 7 trang 126 SGK Hình học 11
Bài tập 7 trang 126 SGK Hình học 11
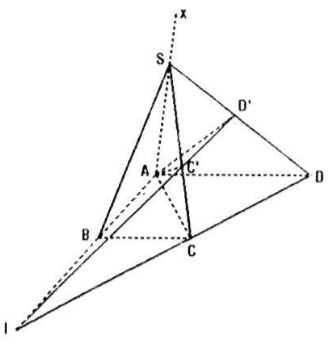
Cho hình thang ABCD vuông tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C', D' lần lượt là hình chiếu vuông góc của A trên SC và SD . Chứng minh rằng :
a) \(\widehat{SBC}=\widehat{SCD}=90^0\)
b) AD’,AC’ và AB cùng nằm trên một mặt phẳng.
c) Chứng minh rằng đường thẳng C’D’ luôn luôn đi qua một điểm cố định kho S di động trên tia Ax.
Câu a:
Dễ thấy \(AD\perp (SAB)\) và do BC // AD.
\(\Rightarrow BC\perp (SAD)\Rightarrow BC\perp SB\Rightarrow \widehat{SBC}=90^0\)
* Ta tính được \(CD=CA=a\sqrt{2}\) mà \(AD = 2a \Rightarrow \Delta ACD\) vuông tại C
\(\Rightarrow CD\perp AC\)
Mặt khác \(SA\perp (ABCD)\Rightarrow CD\perp SA\)
\(\Rightarrow CD\perp (SAC)\Rightarrow CD\perp SC\)
\(\Rightarrow \widehat{SCD}=90^0\)
Câu b:
Theo chứng minh câu a) \(CD\perp (SAC), AC'\subset (SAC)\Rightarrow CD\perp AC'\)
Hơn nữa \(AC'\perp SC\) suy ra:
\(AC'\perp (SCD)\Rightarrow AC'\perp SD\)
Dễ thấy \(AB\perp (SCD)\Rightarrow AB\perp SC\)
Suy ra AC', AD', AB cùng vuông góc với SC ⇒ AC', AD', AB cùng nằm trên mặt phẳng vuông góc với SC hay AC', AD', AB cùng nằm trên một mặt phẳng.
Câu c:
Theo chứng minh câu b) AC', AD', AB cùng nằm trên một mặt phẳng, gọi đó là mặt phẳng \((\alpha )\)
Gọi I là giao điểm của AB và CD ⇒ ID' là giao tuyến của mặt phẳng (SCD) và \((\alpha )\)
Dễ thấy C' \(\in\) SC; C' \(\in\) AC' ⇒ C' nằm trên giao tuyến của \((\alpha )\) và (SCD) ⇒ C', D', I thẳng hàng hay C'D' luôn đi qua I khi S thay đổi trên Ax. (đpcm)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
