Bài tập 8 trang 119 SGK Hình học 11

Bài tập 8 trang 119 SGK Hình học 11

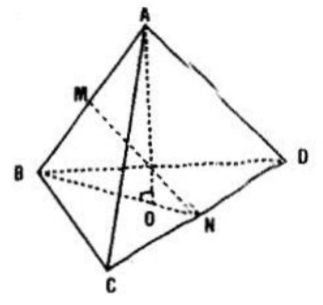
Gọi M, N lần lượt là trung điểm của AB và CD.

Nhận thấy các tam giác đều BCD và ACD bằng nhau

⇒ Các trung tuyến AN và BN bằng nhau.

⇒ \(\Delta NAB\) cân đỉnh N, M là trung điểm AB.

\(\Rightarrow NM\perp AB\)

Chứng minh tương tự ta được \(\Rightarrow NM\perp CD\)

Vậy MN là đường vuông góc chung của AB và CD

Ta tính được \(BN=\frac{a\sqrt{3}}{2}\). Trong tam giác vuông MBN có:

\(MN=\sqrt{BN^2-BM^2}=\sqrt{\frac{3a^2}{4}-\frac{a^2}{4}}=\frac{a\sqrt{2}}{2}\)

Đây cũng chính là khoảng cách giữa hai cạnh đối của tứ diện ABCD.

-- Mod Toán 11