Bài tập 22 trang 111 SGK Hình học 11 NC

Bài tập 22 trang 111 SGK Hình học 11 NC

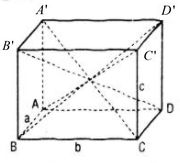
Áp dụng tính chất : “Tổng bình phương hai đường chéo hình bình hành bằng tổng bình phương bốn cạnh của nó” 

Ta có:

\(\begin{array}{*{20}{l}}
{AC{\prime ^2} + A\prime {C^2} = 2(AA{\prime ^2} + A\prime {C^2})}\\
{B\prime {D^2} + BD{\prime ^2} = 2(BB{\prime ^2} + B{D^2})}\\
{ \Rightarrow AC{\prime ^2} + A\prime {C^2} + BD{\prime ^2} + B\prime {D^2}}\\
\begin{array}{l}
 = 2({c^2} + {c^2} + A{C^2} + B{D^2})\\
 = 4({a^2} + {b^2} + {c^2})
\end{array}\\
{ \Rightarrow A\prime C = AC\prime  = B\prime D = BD\prime }
\end{array}\)

⇒ AA’C’C và BB’D’D là các hình chữ nhật 

Từ đó suy ra AA’ ⊥ AC và AA’ ⊥ BD.

Do đó AA’ ⊥ (ABCD), tức hình hộp ABCD.A’B’C’D’ là hình hộp chữ nhật.

-- Mod Toán 11