Bài tập 4 trang 120 SGK Hình học 11 NC

Bài tập 4 trang 120 SGK Hình học 11 NC

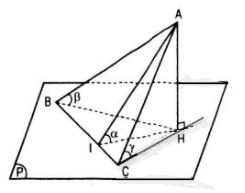
Kẻ AH ⊥ mp(P) và AI ⊥ BC

Thì \(\beta  = \widehat {ABH},\gamma  = \widehat {ACH},\alpha  = \widehat {AIH}\)

Vì ΔABC vuông ở A nên:

\(\begin{array}{*{20}{l}}
{\frac{1}{{A{I^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}}\\
{ \Rightarrow \frac{{A{H^2}}}{{A{I^2}}} = \frac{{A{H^2}}}{{A{B^2}}} + \frac{{A{H^2}}}{{A{C^2}}}}\\
{hay{\mkern 1mu} {\mkern 1mu} {{\sin }^2}\alpha  = {{\sin }^2}\beta  + {{\sin }^2}\gamma }
\end{array}\)

-- Mod Toán 11