200 câu trắc nghiệm Hàm số mũ và Logarit nâng cao !!

A. -11/6

B. 11/6

C. 8/5

D. -8/5

A. $\frac{2017}{567}$

B. $\frac{11}{6}$

C. $\frac{53}{24}$

D. $\frac{2017}{576}$

A. $\mathrm{A}={\mathrm{a}}^{\frac{5}{6}}$

B. $\mathrm{A}={\mathrm{a}}^{\frac{17}{18}}$

C. $\mathrm{A}={\mathrm{a}}^{\frac{5}{9}}$

D. $\mathrm{A}={\mathrm{a}}^{\frac{5}{16}}$

A. 4.

B. 2.

C. 3.

D. 1.

A. A = a - b

B. A = a

C. A = 1/a

D. A = a + b

A. 5

B. $\sqrt{27}$

C. $\sqrt{23}$

D. 25

A. ${\log }_{12}\left(15\right)=\frac{\mathrm{a}+\mathrm{ab}}{\mathrm{b}+2}$

B. ${\log }_{12}\left(15\right)=\frac{\mathrm{a}+\mathrm{ab}}{\mathrm{a}+2}$

C. ${\log }_{12}\left(15\right)=\frac{\mathrm{a}+\mathrm{b}}{\mathrm{ab}+2\mathrm{a}}$

D. ${\log }_{12}\left(15\right)=\frac{\mathrm{a}+\mathrm{b}}{\mathrm{ab}+2\mathrm{b}}$

A. ${\log }_6\left(45\right)=\frac{\mathrm{a}+2\mathrm{ab}}{\mathrm{ab}}$

B. ${\log }_6\left(45\right)=\frac{2{\mathrm{a}}^2-2\mathrm{ab}}{\mathrm{ab}}$

C. ${\log }_6\left(45\right)=\frac{\mathrm{a}+2\mathrm{ab}}{\mathrm{ab}+\mathrm{b}}$

D. ${\log }_6\left(45\right)=\frac{2{\mathrm{a}}^2-2\mathrm{ab}}{\mathrm{ab}+\mathrm{b}}$

A. $\mathrm{A}=\sqrt{\mathrm{ab}}$

B. $\mathrm{A}=\sqrt[3]{\mathrm{ab}}$

C. $\mathrm{A}=\sqrt[6]{\mathrm{ab}}$

D. $\mathrm{A}=\sqrt[6]{\mathrm{a}}-\sqrt[6]{\mathrm{b}}$

A. ${\log }_{15}\left(21\right)=\frac{\mathrm{a}+\mathrm{b}}{\mathrm{ab}+\mathrm{b}}$

B. ${\log }_{15}\left(21\right)=\frac{\mathrm{a}+\mathrm{b}}{\mathrm{a}+1}$

C. ${\log }_{15}\left(21\right)=\frac{\mathrm{a}-\mathrm{b}}{\mathrm{a}+1}$

D. ${\log }_{15}\left(21\right)=\frac{\mathrm{a}-\mathrm{b}}{\mathrm{ab}+\mathrm{b}}$

A. $\frac{\mathrm{ab}+2\mathrm{a}+1}{\mathrm{a}-2}$

B. $\frac{\mathrm{ab}-2\mathrm{a}+1}{\mathrm{a}-2}$

C. $\frac{\mathrm{ab}-2\mathrm{a}+1}{\mathrm{a}+2}$

D. $\frac{\mathrm{ab}+2\mathrm{a}+1}{\mathrm{a}+2}$

A. ${\log }_{15}\left(105\right)=\frac{1+\mathrm{a}+\mathrm{ab}}{(1+\mathrm{a})\mathrm{b}}$

B. ${\log }_{15}\left(105\right)=\frac{1+\mathrm{b}+\mathrm{ab}}{1+\mathrm{a}}$

C. ${\log }_{15}\left(105\right)=\frac{\mathrm{a}+\mathrm{b}+1}{\mathrm{b}(1+\mathrm{a})}$

D. ${\log }_{15}\left(105\right)=\frac{1+\mathrm{b}+\mathrm{ab}}{(1+\mathrm{a})\mathrm{b}}$

A. $\frac{2a+b+1}{a+b}$

B. $\frac{2a+b-1}{a+b}$

C. $\frac{2a-b+1}{a+b}$

D. $\frac{a+b+1}{a+b}$

A. $\frac{1+3pq}{p+q}$

B. $\frac{3pq}{1+3pq}$

C. p.q

D. $\frac{3p+q}{5}$

A. $\frac{3(b+ac)}{c+2}$

B. $\frac{3b+2ac}{c+1}$

C. $\frac{3b+2ac}{c+2}$

D. $\frac{3(b+ac)}{c+1}$

A. $\frac{2ac+1}{abc+2c+1}$

B. $\frac{2ac+1}{abc+2c-1}$

C. $\frac{2ac-1}{abc+2c+1}$

D. $\frac{2ac+1}{abc-2c+1}$

A. ${\log }_{a^2}\left(\sqrt[3]{b^5{c}^4}\right)=\frac{5+4y}{6x}$

B. ${\log }_{a^2}\left(\sqrt[3]{b^5{c}^4}\right)=\frac{20y}{3x}$

C. ${\log }_{a^2}\left(\sqrt[3]{b^5{c}^4}\right)=\frac{5+3y^4}{3x^2}$

D. ${\log }_{a^2}\left(\sqrt[3]{b^5{c}^4}\right)=20x+\frac{20y}{3}$

A. m = 1.

B. m = 1/2 .

C. m = 4.

D.m = 2.

A.. ${\log }_{12}\left(\sqrt{20}\right)=\frac{ab-b+2}{2(a+1)}$

B. ${\log }_{12}\left(\sqrt{20}\right)=\frac{ab+b-2}{2(a+1)}$

C. ${\log }_{12}\left(\sqrt{20}\right)=\frac{ab+b-2}{2(a-1)}$

D. ${\log }_{12}\left(\sqrt{20}\right)=\frac{ab-b+2}{2(a-1)}$

A. ${\log }_{a\sqrt{b}}\left(ab\right)=\frac{1+{\log }_a\left(b\right)}{2+{\log }_a\left(b\right)}$

B. ${\log }_{a\sqrt{b}}\left(ab\right)=\frac{2+{\log }_a\left(b\right)}{1+{\log }_a\left(b\right)}$

C. ${\log }_{a\sqrt{b}}\left(ab\right)=\frac{2+2{\log }_a\left(b\right)}{2+{\log }_a\left(b\right)}$

D. ${\log }_{a\sqrt{b}}\left(ab\right)=\frac{2+{\log }_a\left(b\right)}{2+2{\log }_a\left(b\right)}$

A. $\log (x+y)=\frac{1+\log x+\log y}{2}$

B. log( x + y) = logx + log y + 1

C. log(x + y) = logx + logy - 1

D. log(x + y) = 10( logx + logy)

A. ${\log }_5\left(x+y\right)=\frac{1+{\log }_5\left(xy\right)}{2}$

B. ${\log }_5\left(x+y\right)=\frac{1+{\log }_{5}x+{\log }_{5}y}{2}$

C. log₅(x + y) ² = 1 + log₅( xy)

D. Tất cả đều đúng

A. ${\log }_2\left(\frac{x+y}{14}\right)$=${\log }_2$x+${\log }_2$y

B. ${\log }_2\left(\frac{x+y}{16}\right)$=x+${\log }_2$y

C. ${\log }_2(x+y)=\frac{{\log }_{2}x+{\log }_{2}y}{2}$

D. ${\log }_2\left(x+y\right)=2+\frac{{\log }_2\left(xy\right)}{2}$

A. ${\log }_{abc}\left(x\right)=\frac{pqr}{pq+qr+rp}$

B. ${\log }_{abc}\left(x\right)=pqr$

C. ${\log }_{abc}\left(x\right)=\frac{pqr}{p+q+r}$

D. ${\log }_{abc}\left(x\right)=\frac{pq+qr+rp}{p+q+r}$

A. 0 

B. 1

C. 3

D. 2

A. log_x2012!

B.log_x1002!

C.log_x2011!

D. log_x2011.

A. log_ab

B. $\sqrt{{\log }_{a}b}$

C. ${\log }_a^{2}b$

D. ${\left(\sqrt{{\log }_{a}b}\right)}^3$

A. -1/3

B. 1/3

C. 3

D. - 3

A. $A=\frac{n(n+1)}{{\log }_{a}b}$

B. $A=\frac{n+1}{2{\log }_{a}b}$

C. $A=\frac{n(n+1)}{2{\log }_{a}b}$

D. $A=\frac{n(n-1)}{{\log }_{a}b}$

A. 519

B.  729

C.  469

D.  129

A.   P = 1

B. P = 1/2

C.  P  = 0

D. P = 2

A.  3

B. 4

C. 6

D. 9

A. M = 1/4.

B.  M = 1.

C. M = 1/2.

D.  M = 1/3.

A. 19.

B.  13.

C. 14.

D. 15.

A. $\frac{3-\sqrt{5}}{2}$

B. $\frac{3+\sqrt{5}}{2}$

C. $\frac{-1+\sqrt{5}}{2}$

D. $\frac{-1-\sqrt{5}}{2}$

A. $x=y=\sqrt[3]{2}$

B. $x=\sqrt[3]{2};y=2$

C. x = y= 1

D. $y=\sqrt[3]{2};x=2\sqrt[3]{2}$

A. 2

B. 3

C. 4

D. 5

A.-2log_c+ba.log_c-ba.

B. 3log_c+ba.log_c-ba.

C.2log_c+ba.log_c-ba.

D. Tất cả sai

A. log_ab < 1 < log_ba

B. b < loga1 < log ba

C. log_ab < log_ba < 1

D. log_ba < 1 < log_ab

A.  3log(a+b) = $\frac{1}{2}$(loga+logb)

B. $\log \frac{a+b}{3}=\frac{1}{2}(\log a+\log b)$

C.  2( loga + logb) = log( 7ab) .

D. log(a+b) =$\frac{3}{2}$(loga+logb)

A. ${\log }_{xyz}\left(y^3{z}^2\right)=\frac{3ab+2a}{a+b+1}$

B. ${\log }_{xyz}\left(y^3{z}^2\right)=\frac{3ab+2b}{ab+a+b}$

C. ${\log }_{xyz}\left(y^3{z}^2\right)=\frac{3ab+2a}{ab+a+b}$

D. ${\log }_{xyz}\left(y^3{z}^2\right)=\frac{3ab+2b}{a+b+1}$

A. log$\sqrt{2a+3b}$=log$\sqrt{a}$+2log$\sqrt{b}$

B. $\frac{1}{4}$log(2a+3b)=3log a+2logb

C. log$\left(\frac{2a+3b}{5}\right)$=$\frac{1}{2}$(loga+logb)

D. log$\left(\frac{2a+3b}{4}\right)$=$\frac{1}{2}$(loga+logb)

A. log_{2$\left(\frac{x+2y}{4}\right)$}=log₂x-log₂y

B. log2(x+2y)=2+$\frac{1}{2}$(log₂x+log₂y)

C. log₂(x + 2y) = log₂x+log₂y+1

D. 4log₂( x + 2y) = log₂x + log₂y.

A. ${\log }_{\frac{a}{b}}^2\frac{c}{b}.{\log }_{\frac{{\displaystyle b}}{{\displaystyle c}}}^2\frac{{\displaystyle a}}{{\displaystyle c}}.{\log }_{\frac{{\displaystyle c}}{{\displaystyle a}}}^2\frac{{\displaystyle b}}{{\displaystyle a}}=1$

B. ${\log }_{\frac{a}{b}}^2\frac{c}{b}.{\log }_{\frac{{\displaystyle b}}{{\displaystyle c}}}^2\frac{{\displaystyle a}}{{\displaystyle c}}.{\log }_{\frac{{\displaystyle c}}{{\displaystyle a}}}^2\frac{{\displaystyle b}}{{\displaystyle a}}>1$

C. ${\log }_{\frac{a}{b}}^2\frac{c}{b}.{\log }_{\frac{{\displaystyle b}}{{\displaystyle c}}}^2\frac{{\displaystyle a}}{{\displaystyle c}}.{\log }_{\frac{{\displaystyle c}}{{\displaystyle a}}}^2\frac{{\displaystyle b}}{{\displaystyle a}}>-1$

D. ${\log }_{\frac{a}{b}}^2\frac{c}{b}.{\log }_{\frac{{\displaystyle b}}{{\displaystyle c}}}^2\frac{{\displaystyle a}}{{\displaystyle c}}.{\log }_{\frac{{\displaystyle c}}{{\displaystyle a}}}^2\frac{{\displaystyle b}}{{\displaystyle a}}<1$ 

A. $\ln \frac{a+b}{4}=\frac{\ln {\displaystyle a}{\displaystyle +}{\displaystyle \ln }{\displaystyle b}}{2}$

B. 2log₂(a + b) = 4 + log₂a + log₂b.

C. 2log₄(a + b) = 4 + log₄a + log₄b.

D. $2\log \frac{a+b}{4}=\log a+\log b$

A. m = 2

B. -2 < m < 2

C.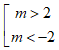

D. m < 2

A. m > -3

B. m < 3

C. $m\le -3$

D. $m\ge -3$

A. 1

B. 2

C. log₂5

D. log₂3

A. m > -4

B. m $\ge$ -1/4

C. m < -4

D. m > -1/4

A. 0 < a < 4

B. a > 0

C. a > 4

D. $a\in \varnothing$

A. $\mathrm{m}\ge \frac{1}{4}$

B. m > 1/4

C. m < -1/4

D. m > 0

A. 1

B. 5

C. 10

D. 13

A. $y\text{'}=\frac{4\ln \left(x^2+1\right)}{3y^2\left(x^2+1\right)}$

B. $y\text{'}=\frac{2x\ln \left(x^2+1\right)}{3y^2\left(x^2+1\right)}$

C. $y\text{'}=\frac{4x\ln \left(x^2+1\right)}{3y^2\left(x^2+1\right)}$

D. $y\text{'}=\frac{2\ln \left(x^2+1\right)}{3y^2\left(x^2+1\right)}$

A. x/y = 4

B. x/y = 3

C. x/y = 5

D. x/y = 2

A. y = ln( x - 1)

B. $y={\log }_{\frac{1}{2}}\left(x-1\right)$

C. y = 2^x-1

D. $y={\left(\frac{1}{2}\right)}^{x-1}$

A. 15

B. -12

C. -15

D. -10

A. a > b > 1

B. b > a > 1

C. 1 > a > b > 0

D. 1 > b > a > 0

A. $0<\beta <1<\alpha$

B. $\beta <0<1<\alpha$

C. $0<\alpha <1<\beta$

D. $\alpha <0<1<\beta$

A. 7

B. 9

C. 6

D. 10

A. m > 2

B. m > 5

C. m < 3

D. m < 0

A. 1 < m < 2

B. $m\in \left[-\frac{1}{2};\frac{1}{2}\right]$

C. $m\in \left[-\frac{1}{2};\frac{1}{2}\right]\cup \left(1;2\right) \backslash \left\{0\right\}$

D. 1 ≤ m ≤ 2

A. ab² = 1

B. b = 3a

C. a³b = 1

D. ab³ = 1

A. $D=\left(0;+\infty \right)$

B. $D=\left(3;+\infty \right)$

C. $D=\left(1;+\infty \right)$

D. $D=\left(\frac{1}{3};+\infty \right)$

A. $D=\left(\sqrt{e};+\infty \right)$

B. $D=\left(0;+\infty \right)$

C. $D=\left(\frac{e}{2};+\infty \right)$

D. $D=\left(-\infty ;-\sqrt{e}\right)\cup \left(\sqrt{e};+\infty \right)$

A. $y\text{'}=\frac{e^{\sqrt{x}}+e^{-\sqrt{x}}}{2\sqrt{x}}$

B. $y\text{'}=\frac{e^{\sqrt{x}}-e^{-\sqrt{x}}}{2\sqrt{x}}$

C. $y\text{'}=\frac{e^{\sqrt{x}}-e^{-\sqrt{x}}}{\sqrt{x}}$

D. $y\text{'}=\frac{e^{\sqrt{x}}+e^{-\sqrt{x}}}{\sqrt{x}}$

A. $y\text{'}=\frac{-1}{x\left(\ln 3-\ln 2\right)}$

B. $y\text{'}=\frac{1}{\left|x\right|\left(\ln 3-\ln 2\right)}$

C. $y\text{'}=\frac{1}{x\left(\ln 3-\ln 2\right)}$

D. $y\text{'}=\frac{3}{2x\left(\ln 3-\ln 2\right)}$

A. $y\text{'}=\frac{1}{\left(2x-1\right)\ln 2}$

B. $y\text{'}=\frac{4}{\left(2x-1\right)\ln 2}$

C. $y\text{'}=\frac{2}{\left(2x-1\right)\ln 2}$

D. $y\text{'}=\frac{1}{\left|2x-1\right|\ln 2}$

A. $\frac{\cos \left(x^2+1\right)-\ln 2.\sin \left(x^2+1\right)}{2^x}$

B. $\frac{\cos \left(x^2+1\right)-\ln 2.\sin \left(x^2+1\right)}{4^x}$

C. $\frac{2x\cos \left(x^2+1\right)-\ln 2.\sin \left(x^2+1\right)}{2^x}$

D. $\frac{-2x\cos \left(x^2+1\right)-\ln 2.\sin \left(x^2+1\right)}{2^x}$

A. $y\text{'}=\frac{1}{\left|x-2\right|}+2^x\ln 2$

B. $y\text{'}=\frac{1}{\left|x-2\right|}+2^x$

C. $y\text{'}=\frac{1}{x-2}+2^x\ln 2$

D. $y\text{'}=\frac{1}{x-2}+2^x$

A. $y\text{'}=\frac{x+1}{2\sqrt{x^2+2x+3}}$

B. $y\text{'}=\frac{2x+2}{\sqrt{x^2+2x+3}}$

C. $y\text{'}=\frac{x+1}{\sqrt{x^2+2x+3}}$

D. $y\text{'}=\frac{x+1}{x^2+2x+3}$

A. $y\text{'}=\frac{-1}{x^2-1}$

B. $y\text{'}=\frac{1}{x^2-1}$

C. $y\text{'}=\frac{1}{2\left(x^2-1\right)}$

D. $y\text{'}=\frac{-1}{2\left(x^2-1\right)}$

A. $f\text{'}\left(x\right)=\frac{1}{\sqrt{x^2+1}}$

B. $f\text{'}\left(x\right)=\frac{1}{x+\sqrt{x^2+1}}$

C. $f\text{'}\left(x\right)=\frac{1}{x+\sqrt{x^2+1}}\left(1+\frac{1}{2\sqrt{x^2+1}}\right)$

D. $f\text{'}\left(x\right)=\frac{2x}{\sqrt{x^2+1}}$

A. $\underset{\mathrm{ℝ}}{min}y=2\sqrt{2};\underset{\mathrm{ℝ}}{max}y=3$

B. $\underset{\mathrm{ℝ}}{min}y=2;\underset{\mathrm{ℝ}}{max}y=3$

C. $\underset{\mathrm{ℝ}}{min}y=3;\underset{\mathrm{ℝ}}{max}y=3\sqrt{2}$

D. $\underset{\mathrm{ℝ}}{min}y=2;\underset{\mathrm{ℝ}}{max}y=3\sqrt{2}$

A. $\underset{\left[-1;1\right]}{min} y=-\frac{3}{4};\underset{\left[-1;1\right]}{max} y=2$

B. $\underset{\left[-1;1\right]}{min} y=-\frac{3}{4};\underset{\left[-1;1\right]}{max} y=0$

C. $\underset{\left[-1;1\right]}{min} y=-1;\underset{\left[-1;1\right]}{max} y=1$

D. $\underset{\left[-1;1\right]}{min} y=-1;\underset{\left[-1;1\right]}{max} y=0$

A. $\underset{\left[0;1\right]}{min}y=2\sqrt{5};\underset{\left[0;1\right]}{max}y=6$

B. $\underset{\left[0;1\right]}{min}y=2\sqrt{5};\underset{\left[0;1\right]}{max}y=5$

C. $\underset{\left[0;1\right]}{min}y=2;\underset{\left[0;1\right]}{max}y=6$

D. $\underset{\left[0;1\right]}{min}y=2;\underset{\left[0;1\right]}{max}y=5$

A. $S_{min}=\frac{9\sqrt{11}}{9}-1$

B. $S_{min}=\frac{9\sqrt{11}-9}{9}$

C. $S_{min}=\frac{2\sqrt{11}-9}{9}$

D. Đáp án khác

A.12

B.14

C. 8

D.16

A.19

B.13

C.14

D.15

A. 0

B. 1

C. 2

D. 3

A. 2.

B. 1.

C. 4.

D. 3.

A. 1

B. 3

C. 2

D. 0

A. 45

B. 96

C. 39

D. 126

A. $\mathrm{T}=\mathrm{\pi }$

B. $\mathrm{T}=\frac{3\mathrm{\pi }}{2}$

C. $\mathrm{T}=6\mathrm{\pi }$

D. T = 0

A. 0.

B. 2.

C. -2.

D. 1.

A. S = 1

B. S = -1

C. S = 3

D. S = 0

A. 1.

B. 2.

C. 3.

D. 0.

A. $x_0\in \left(-\infty ;-1\right)$

B. $x_0\in \left[-1;1\right]$

C. $x_0\in \left(1;\sqrt{15}\right)$

D. $x_0\in \left[\sqrt{15};+\infty \right]$

A. 1

B. 2

C. 3

D. 4

A. 3x₁ - 2x₂ = log₃8.

B. 2x₁ - 3x₂ = log₃8.

C. x₁ + x₂ = log₃486.

D. 3x₁ + 2x₂ = log₃54.

A. 2

B. 6

C. 4

D. 0

A. 0 < a < 4/5

B. 5 < a < 9

C. 4/5 < a < 12/5

D. 3 < a < 7/2

A. $x=\frac{1-{\log }_{2+\sqrt{5}} 3}{3}$

B. $x=\frac{-1+{\log }_{2+\sqrt{5}} 3}{3}$

C. $x=\frac{1-{\log }_{2+\sqrt{5}} 3}{5}$

D. $x=\frac{-1+{\log }_{2+\sqrt{5}} 3}{5}$

A. 4

B. 3

C. 7

D. 6

A. 1.

B. 2.

C. 3.

D. 0.

A. f(x) = 1 khi $\left(x+1\right){\log }_{5}3+x^2=0$

B. f(x) = 1 khi $\left(x+1\right){\log }_{\frac{1}{5}}3-x^2=0$

C. f(x) = 1 khi x² log₃5 = 0.

D. f(x) = 1 khi (x + 1)ln3 + x²ln5 = 0.

A.40

B.50

C.60

D.70

A. T > 1

B. T = 1

C. -0, 5 < T

D. T < -0,5

A. 0.

B. 1.

C. 2.

D. 4.

A. 0

B. 1

C. 2

D. 3

A. $P=\frac{\sqrt{26}}{5}$

B. $P=\sqrt{26}$

C. P = 26

D. $P=\frac{26}{25}$

A. 95

B. 100

C. 36

D. 32

A. 4

B. 2

C. 3

D. 1

A. 6

B. 5

C. 3

D. 4

A. $x=-{\log }_{2+\sqrt{3}} 2$

B. $x={\log }_{2+\sqrt{3}} 2$

C. $x=-{\log }_{2+\sqrt{3}} 4$

D. $x={\log }_{2+\sqrt{3}} 4$

A. log₂24

B. log₂12

C. log₂18

D. log₂6

A. 2 - 4log₆2

B. 2 -log₆3

C. 2 - 4log₆3

D. 2 + 4log₆3

A. 4

B. 2

C. 3

D. 1

A. 2611

B. 2681

C. 2422

D. 2429

A. log₅18

B. log₅9

C. log₅3

D. log₅15

A. 2

B. 3

C. 1

D.  4

A. Có nghiệm.

B. Có vô số nghiệm.

C. Có  nghiệm.

D. Không có nghiệm.

A. Phương trình (1)  có nghiệm duy nhất.

B. Phương trình (1) vô nghiệm.

C. Phương trình (1) có tổng các nghiệm bằng 0.

D. Phương trình (1) có nhiều hơn hai nghiệm.

A. 1.

B. 2.

C. 3.

D. 4.

A. 1.

B. 2.

C. 0.

D. 3.

A. 1.

B. 2.

C. 3.

D. 4.

A. $x=\mathrm{\pi }$

B. $x=\frac{\mathrm{\pi }}{4}$

C. $x=\frac{\mathrm{\pi }}{2}$

D. $x=\frac{3\mathrm{\pi }}{4}$

A. 2.

B. 0.