Bài tập 2.3 trang 47 SBT Hình học 12

Bài tập 2.3 trang 47 SBT Hình học 12

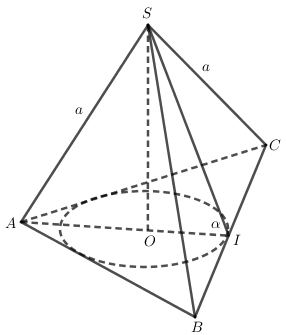
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC.

Theo giả thiết ta có \(SA = SB = SC = a\) và \(\widehat {SIO} = \alpha \).

Đặt \(OI = r,SO = h\), ta có AO = 2r và \(\left\{ \begin{array}{l}
h = r\tan \alpha \\
{a^2} = {h^2} + 4{r^2}
\end{array} \right.\) (vì \(S{A^2} = S{O^2} + A{O^2}\))

Do đó \({a^2} = {r^2}{\tan ^2}\alpha  + 4{r^2} = {r^2}({\tan ^2}\alpha  + 4)\)

Vậy \(r = \frac{a}{{\sqrt {{{\tan }^2}\alpha  + 4} }}\)

Hình nón nội tiếp có đường sinh là: \(l = SI = \frac{r}{{\cos \alpha }} = \frac{a}{{\cos \alpha \sqrt {{{\tan }^2}\alpha  + 4} }}\)

Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:

\({S_{xq}} = \pi rl = \pi .\frac{a}{{\sqrt {{{\tan }^2}\alpha  + 4} }}.\frac{a}{{\cos \alpha \sqrt {{{\tan }^2}\alpha  + 4} }} = \frac{{\pi {a^2}}}{{\cos \alpha ({{\tan }^2}\alpha  + 4)}}\)

-- Mod Toán 12