Bài tập 6 trang 65 SGK Hình học 12 NC

Bài tập 6 trang 65 SGK Hình học 12 NC

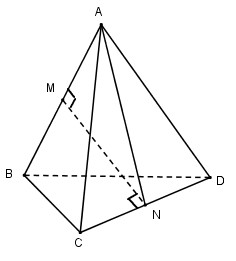
Gọi M, N lần lượt là trung điểm hai cạnh AB và CD của tứ diện đều ABCD.

I là trung điểm của MN thì I cách đều 6$6$ cạnh tứ diện nên I là tâm mặt cầu tiếp xúc với các cạnh của tứ diện đều.

Bán kính mặt cầu: \(R = \frac{{MN}}{2}\)

Ta có: 

\(\begin{array}{l}
M{N^2} = A{N^2} - M{A^2}\\
 = A{D^2} - N{D^2} - M{A^2}\\
 = {a^2} - \frac{{{a^2}}}{4} - \frac{{{a^2}}}{4} = \frac{{{a^2}}}{2}\\
 \Rightarrow MN = \frac{{a\sqrt 2 }}{2} \Rightarrow R = \frac{{a\sqrt 2 }}{4}
\end{array}\)

Chọn (B).

-- Mod Toán 12