Bài tập 3 trang 50 SGK Hình học 12

Bài tập 3 trang 50 SGK Hình học 12

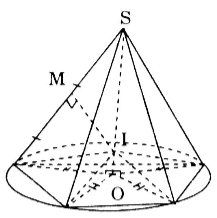
Gọi O là hình chiếu của S lên mặt đáy. Do các cạnh bên của hình chóp bằng nhau nên O cách đều các đỉnh của đa giác đáy. Như vậy đáy của hình chóp là một đa giác nội tiếp đường tròn tâm O và nhận SO làm trục.

Gọi I là giao điểm của SO và mặt phẳng trung trực của một cạnh bên, ta có I cách đều tất cả các đỉnh của hình chóp một đoạn r = SI.

Vậy hình chóp luôn nội tiếp một mặt cầu S(I; r).

-- Mod Toán 12