Trang chủ
Lớp 12
Toán Lớp 12 SGK Cũ
Chương 2: Mặt Nón, Mặt Trụ, Mặt Cầu
Bài tập 9 trang 65 SGK Hình học 12 NC
Bài tập 9 trang 65 SGK Hình học 12 NC
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 9 trang 65 SGK Hình học 12 NC
Cho hai điểm phân biệt A, B cố định và phân biệt. Một đường thẳng l thay đổi luôn đi qua A và cách B một khoảng AB2. Gọi H là hình chiếu của B trên l. Tập hợp điểm H là:
(A) Một mặt phẳng
(B) Một mặt trụ
(C) Một mặt nón
(D) Một đường tròn
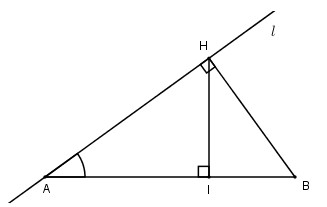
\(\sin \widehat {HAB} = \frac{{BH}}{{AB}} = \frac{1}{2} \Rightarrow \widehat {HAB} = {30^0}\)
Tập hợp l là mặt nón có trục AB, đường sinh l, góc ở đỉnh là 600. Gọi I là hình chiếu của H lên AB.
Ta có: \(BI = BH.\cos {60^0} = \frac{{AB}}{4} \)
\(\Rightarrow I\) cố định.
⇒ H thuộc mặt phẳng qua I vuông góc với AB. Vậy tâp hợp H là đường tròn.
Chọn (D).
-- Mod Toán 12
Copyright © 2021 HOCTAP247
