Trang chủ
Lớp 12
Toán Lớp 12 SGK Cũ
Chương 2: Mặt Nón, Mặt Trụ, Mặt Cầu
Bài tập 23 trang 68 SGK Hình học 12 NC
Bài tập 23 trang 68 SGK Hình học 12 NC
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 23 trang 68 SGK Hình học 12 NC
Cho hình trụ có bán kính đáy bằng R, chiều cao cũng bằng R. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy, mp(ABCD) không vuông góc với mặt phẳng đáy của hình trụ. Diện tích hình vuông đó là
(A) \(\frac{{5{R^2}}}{2}\)
(B) \(5{R^2}\)
(C) \(\frac{{5{R^2}\sqrt 2 }}{2}\)
(D) \(5{R^2}\sqrt 2 \)
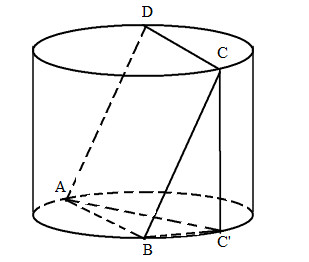
Gọi C’ là hình chiếu của C trên đáy hình trụ.
Khi đó ta có \(AB \bot BC'\) (vì \(AB \bot BC\)).
Vậy AC′ = 2R
Ta có:
\(\begin{array}{l}
B{C^{\prime 2}} = 4{R^2} - A{B^2} = A{B^2} - {R^2}\\
\Rightarrow A{B^2} = \frac{5}{2}{R^2}.
\end{array}\)
Chọn (A).
-- Mod Toán 12
Copyright © 2021 HOCTAP247
