Bài tập 10 trang 40 SGK Hình học 12

Bài tập 10 trang 40 SGK Hình học 12

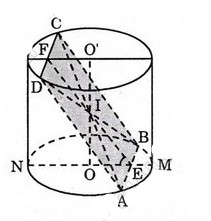
Do tính chất đối xứng của (ABCD) nên (ABCD) cắt OO′ tại trung điểm I của OO′. I cũng là giao điểm của hai đường chéo AC, BD

Xét tam giác vuông IOB ta có: IB²=IO²+OB²

\(\begin{array}{l}
 \Rightarrow IB = \sqrt {{{\left( {\frac{r}{2}} \right)}^2} + {r^2}}  = \frac{{r\sqrt 5 }}{2}\\
 \Rightarrow AC = BD = 2IB = r\sqrt 5 
\end{array}\)

Do ABCD là hinh vuông nên \(AB = \frac{{AC}}{{\sqrt 2 }} = \frac{{r\sqrt {10} }}{2}\)

Vậy \({S_{ABCD}} = A{B^2} = \frac{{5{r^2}}}{2}\)

Gọi E là trung điểm của AB

⇒ OE ⊥ AB, IE ⊥ AB

\( \Rightarrow \widehat {IEO}\) là góc giữa (ABCD)$(ABCD)$  và mặt đáy của hình trụ.

Ta có: \(IE = \frac{1}{2}AD = \frac{{r\sqrt {10} }}{4},OI = \frac{r}{2}\)

Xét tam giác vuông IOE có: 

\(\begin{array}{l}
OE = \sqrt {I{E^2} - O{I^2}} \\
 = \sqrt {{{\left( {\frac{{r\sqrt {10} }}{4}} \right)}^2} - {{\left( {\frac{r}{2}} \right)}^2}}  = \frac{{r\sqrt 6 }}{4}\\
\cos \widehat {IEO} = \frac{{OE}}{{IE}} = \frac{{\sqrt {15} }}{5}
\end{array}\)

-- Mod Toán 12