Trang chủ
Lớp 12
Toán Lớp 12 SGK Cũ
Chương 2: Mặt Nón, Mặt Trụ, Mặt Cầu
Bài tập 13 trang 66 SGK Hình học 12 NC
Bài tập 13 trang 66 SGK Hình học 12 NC
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 13 trang 66 SGK Hình học 12 NC
Cho hình lập phương ABCD.A’B’C’D’ có cạnh a. Diện tích xung quanh của hình nón tròn xoay sinh bởi đường gấp khúc AC’A’ khi quay quanh AA’ bằng:
(A) \(\pi {a^2}\sqrt 6 \)
(B) \(\pi {a^2}\sqrt 3 \)
(C) \(\pi {a^2}\sqrt 2 \)
(D) \(\pi {a^2}\sqrt 5 \)
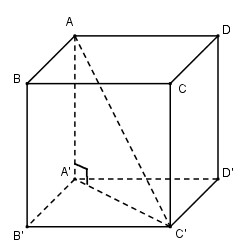
Hình nón tròn xoay sinh bởi đường gấp khúc AC’A’ khi quay quanh AA′ có bán kính đáy \(A'C' = a\sqrt 2 \) và độ dài đường sinh \(AC' = a\sqrt 3 \) nên diện tích xung quanh của hình nón là:
\({S_{xq}} = \frac{1}{2}2\pi a\sqrt 2 .a\sqrt 3 = \pi {a^2}\sqrt 6 \)
Chọn (A).
-- Mod Toán 12
Copyright © 2021 HOCTAP247
