Trang chủ
Lớp 12
Toán Lớp 12 SGK Cũ
Chương 2: Mặt Nón, Mặt Trụ, Mặt Cầu
Bài tập 9 trang 49 SGK Hình học 12
Bài tập 9 trang 49 SGK Hình học 12
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 9 trang 49 SGK Hình học 12
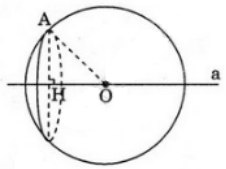
Cho một điểm A cố định và một đường thẳng α cố định không đi qua A. Gọi O là một điểm thay đổi trên \(\alpha\). Chứng minh rằng các mặt cầu tâm O và bán kính r = OA luôn luôn đi qua một đường tròn cố định.
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.
Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.
Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.
-- Mod Toán 12
Copyright © 2021 HOCTAP247