Bài tập 11 trang 66 SGK Hình học 12 NC
Bài tập 11 trang 66 SGK Hình học 12 NC
Một hình trụ có bán kính đáy bằng a, đường cao \({\rm{OO}}' = a\sqrt 3 \). Một đoạn thẳng AB thay đổi sao cho góc giữa AB và trục hình trụ bằng 300. A, B thuộc hai đường tròn đáy của hình trụ. Tập hợp các trung điểm I của AB là:
(A) Một mặt trụ
(B) Một mặt cầu
(C) Một đường tròn
(D) Một mặt phẳng.
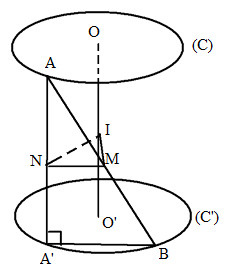
Gọi A′ là hình chiếu của A xuống mặt phẳng đáy thì AA′ = OO′. Gọi I, M, N lần lượt là trung điểm của OO′, AB và AA′.
Ta có: IA = IB và \(IM \bot AB\).
Mp(IMN) qua I và song song với hai mặt phẳng đáy.
Ta có:
\(\begin{array}{l}
MN = AN.\tan {30^0} = \frac{{a\sqrt 3 }}{2}.\frac{1}{{\sqrt 3 }} = \frac{a}{2}\\
\Rightarrow MI = \sqrt {N{I^2} - M{N^2}} \\
= \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}
\end{array}\)
Vậy tập hợp trung điểm M của AB là đường tròn tâm I bán kính \(\frac{{a\sqrt 3 }}{2}\) nằm trong mp(IMN).
Chọn (C).
-- Mod Toán 12
Copyright © 2021 HOCTAP247
