Bài tập 21 trang 67 SGK Hình học 12 NC

Bài tập 21 trang 67 SGK Hình học 12 NC

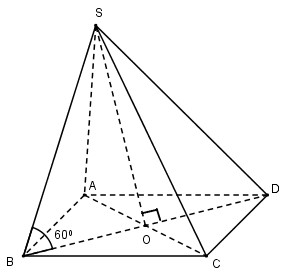
Bán kính đường tròn đáy của hình nón ngoại tiếp hình chóp là

\(\begin{array}{l}

R = \frac{{a\sqrt 2 }}{2},\cos {60^0} = \frac{{BO}}{{SB}}\\

\Rightarrow SB = \frac{{BO}}{{\cos {{60}^0}}} = 2\frac{{a\sqrt 2 }}{2} = a\sqrt 2 

\end{array}\)

Diện tích xung quanh hình nón:

\({S_{xq}} = \frac{1}{2}.2\pi Rl = \pi \frac{{a\sqrt 2 }}{2}a\sqrt 2  = \pi {a^2}\)

Diện tích hình tròn đáy hình nón là:

\({S_d} = \pi {R^2} = \pi \frac{{{a^2}}}{2}\)

Diện tích toàn phần:

\({S_{tp}} = {S_{xq}} + {S_d} = \pi {a^2} + \frac{{\pi {a^2}}}{2} = \frac{{3\pi {a^2}}}{2}\)

Chọn (A).

-- Mod Toán 12